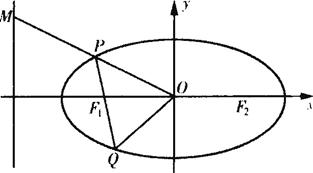
题目内容

设过椭圆C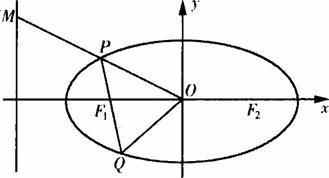：+y2=1(a＞1)中心O的直线与椭圆C的左准线交于点M，与椭圆C交于点P，过点P与左焦点F1(-c，0)的直线l：x=my-c交椭圆C于另一点Q.

(Ⅰ)若=且M的纵坐标为时，求椭圆C的方程；

(Ⅱ)当且椭圆C的离心率在()变化时,求实数m的取值范围.

解：(Ⅰ)设O(0,0)、P(x0,y0),M(-)(x0＜0),

∵,则P是OM的中点, 

∵M的纵坐标为,P(x0,y0)在椭圆上,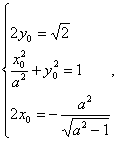

解之：x0=-1,a2=2,则椭圆C的方程为+y2=1, 

(Ⅱ)由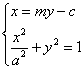消x整理得:(a2+m2)y2-2cmy-1=0,  ①

设点P(x1,y1)、Q(x2,y2),则y1+y2=,y1·y2=, 

∴=(x1,y1),=(x2,y2),且·=x1·x2+y1·y2,

又x1·x2  =(my1-c)(my2-c)=m2y1·y2-cm(y1+y2)+c2=,

∴·=

化简得：3a4-2a2-2=a2m2,∴m2=3a2--2

∵e∈(,),则＜e2＜,＜,＜a2＜2, 

设t=a2,则m2=3t--2在(,2)上是增函数,

∴＜m2＜3,...-＜m＜-或＜m＜.

练习册系列答案
相关题目
椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的一个焦点F1（-2，0），右准线方程x=8．
（1）求椭圆C的方程；
（2）若M为右准线上一点，A为椭圆C的左顶点，连接AM交椭圆于点P，求
PM
AP
的取值范围；
（3）设圆Q：（x-t）2+y2=1（t＞4）与椭圆C有且只有一个公共点，过椭圆C上一点B作圆Q的切线BS、BT，切点为S，T，求
BS
•
BT
的最大值．
已知直线l：y=2x-
3
与椭圆C：
x2
a2
+y2=1 （a＞1）交于P、Q两点，
（1）设PQ中点M（x0，y0），求证：x0＜
3
2
；
（2）以PQ为直径的圆过椭圆C的右顶点A．求椭圆C的方程．
（2012•杭州二模）已知椭圆
x2
a2
+
y2
b2
=1 (a ＞ b ＞ 0)上任一点P到两个焦点的距离的和为2
3
，P与椭圆长轴两顶点连线的斜率之积为-
2
3
．设直线l过椭圆C的右焦点F，交椭圆C于两点A（x1，y1），B（x2，y2）．
（Ⅰ）若
OA
•
OB
=
4
tan∠AOB
（O为坐标原点），求|y1-y2|的值；
（Ⅱ）当直线l与两坐标轴都不垂直时，在x轴上是否总存在点Q，使得直线QA、QB的倾斜   角互为补角？若存在，求出点Q的坐标；若不存在，请说明理由．
设过椭圆C：+y2=1(a＞1)中心O的直线与椭圆C的左准线交于点M，与椭圆C交于点P，过点P与左焦点F1(-c，0)的直线l：x=my-c交椭圆C于另一点Q．

(Ⅰ)若且M的纵坐标为时，求椭圆C的方程；

(Ⅱ)当椭圆C的离心率e=，且时，求m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网