题目内容
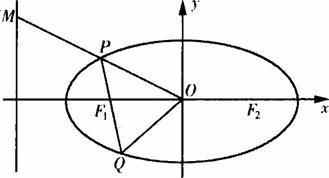
设过椭圆C:(Ⅰ)若![]() 且M的纵坐标为
且M的纵坐标为![]() 时,求椭圆C的方程;
时,求椭圆C的方程;
(Ⅱ)当椭圆C的离心率e=![]() ,且
,且![]() 时,求m的值.
时,求m的值.
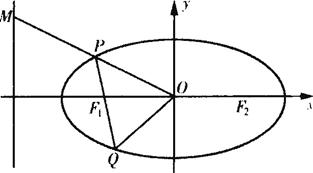
解:(Ⅰ)设O(0,0),P(x0,y0),M(![]() )(x0<0),
)(x0<0),
∵![]() ,则P是OM的中点,
,则P是OM的中点,
∵M的纵坐标为![]() ,P(x0,y0)在椭圆上,
,P(x0,y0)在椭圆上,
∴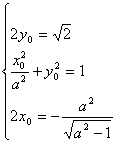 ,
,
解之:x0=-1,a2=2,则椭圆C的方程为![]() +y2=1,
+y2=1,
(Ⅱ)由e=![]() 可知:e=
可知:e=![]() a2=3,c=
a2=3,c=![]() ,
,
∵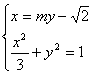 ,消去x整理得:(3+m2)y2-2
,消去x整理得:(3+m2)y2-2![]() my-1=0①
my-1=0①
设点P(x1,y1),Q(x2,y2),则y1+y2=![]() ,
,
y1·y2=![]() ,
,
∴![]() =( x1,y1),
=( x1,y1), ![]() =( x2,y2),∴
=( x2,y2),∴![]() ·
·![]() =x1·x2+ y1·y2,
=x1·x2+ y1·y2,
又x1·x2=(m y1-![]() )(my2-
)(my2-![]() )=m2y1·y2-
)=m2y1·y2-![]() m(y1+y2)+2
m(y1+y2)+2
=![]() ,
,
∴![]() ·
·![]() =
=![]() ,
,
解得m2=![]() ,从而m=±
,从而m=±![]() .
.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目