题目内容

13．设f（x）=3x2ex，则f′（2）=（　　）
A．12eB．12e2C．24eD．24e2

分析 求函数的导数即可得到结论．

解答 解：f′（x）=6xex+3x2ex，
∴f′（2）=12e2+12e2=24e2．
故选：D．

点评 本题主要考查导数的计算，要求熟练掌握常见函数的导数公式，比较基础．

练习册系列答案
相关题目
7．函数f（x）=$\sqrt{x\sqrt{x\sqrt{x}}}$（x＞0）的导数为f′（x）=$\frac{7}{8}$•${x}^{-\frac{1}{8}}$．
4．已知实数x，y满足x2+y2-4x+2=0，则x2+（y-2）2的最小值是（　　）
A．$\sqrt{2}$B．$2\sqrt{2}$C．2D．8
1．600°角是第（　　）象限的角．
A．一B．二C．三D．四
8．已知a、b是异面直线，直线c∥直线a，则直线c与直线b（　　）
A．异面B．相交C．平行D．不可能平行
18．设三棱锥O-ABC中，$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，G是△ABC的重心，则$\overrightarrow{OG}$等于（　　）
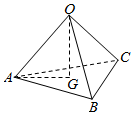
A．$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$B．$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$C．$\frac{1}{2}$（$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$）D．$\frac{1}{3}$（$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$）
5．已知函数f（x）=lg（ax2+ax+2）（a∈R）．
（1）若a=-1，求f（x）的单调区间；
（2）若函数f（x）的定义域为R，求实数a的取值范围．
2．已知函数：$f（x）=1+x-\frac{x^2}{2}+\frac{x^3}{3}-\frac{x^4}{4}+…+\frac{{{x^{2015}}}}{2015}$，$g（x）=1-x+\frac{x^2}{2}-\frac{x^3}{3}+\frac{x^4}{4}-…-\frac{{{x^{2015}}}}{2015}$，设函数F（x）=f（x+3）•g（x-5），且函数F（x）的零点均在区间[a，b]（a＜b，a，b∈Z）内，则b-a的最小值为（　　）
A．8B．9C．10D．11
3．设{an}是公比为q的等比数列，则“q＞1”是“{an}”为递增数列的既不充分也不必要条件（用“充分且不必要条件”，“必要且不充分条件”，“充分必要条件”，“既不充分也不必要条件”填空）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网