题目内容
设曲线f(x)=lnx-
x在点(1,-
)处的切线与直线ax-y+1=0垂直,则a=( )
| 1 |
| 2 |
| 1 |
| 2 |
分析:由f(x)=lnx-
x,知f′(x)=
-
,故曲线f(x)=lnx-
x在点(1,-
)处的切线的斜率k=f′(1)=1-
=
,由曲线f(x)=lnx-
x在点(1,-
)处的切线与直线ax-y+1=0垂直,能求出a的值.
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:∵f(x)=lnx-
x,
∴f′(x)=
-
,
∴曲线f(x)=lnx-
x在点(1,-
)处的切线的斜率k=f′(1)=1-
=
,
∵曲线f(x)=lnx-
x在点(1,-
)处的切线与直线ax-y+1=0垂直,
∴直线ax-y+1=0的斜率k′=a=-2.
故选C.
| 1 |
| 2 |
∴f′(x)=
| 1 |
| x |
| 1 |
| 2 |
∴曲线f(x)=lnx-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∵曲线f(x)=lnx-
| 1 |
| 2 |
| 1 |
| 2 |
∴直线ax-y+1=0的斜率k′=a=-2.
故选C.
点评:本题考查导数的几何意义的求法,是基础题.解题时要认真审题,仔细解答,注意直线与直线垂直的性质的灵活运用.

练习册系列答案
相关题目
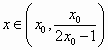 使f(x)>x2-ln(1+ex)成立.
使f(x)>x2-ln(1+ex)成立.