题目内容
已知a>0,函数f(x)=ln(2-x)+ax.?(1)设曲线y=f(x)在点(1,f(1))处的切线为l,若l与圆(x+1)2+y2=1相切,求a的值;?
(2)求函数f(x)的单调区间.
解析:(1)依题意,有x<2,f′(x)=a+![]() ,?
,?
过(1,f(1))点的直线的斜率为a-1,所以过(1,f(1))点的直线方程为y-a=(a-1)(x-1).?
又已知圆圆心为(-1,0),半径为1,?
依题意,有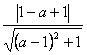 =1.解之,得a=1.?
=1.解之,得a=1.?
(2)f′(x)=![]() =a[x-(2-
=a[x-(2-![]() )]
)]![]() ,?
,?
当a>0时,2-![]() <2,?
<2,?
令f′(x)>0,解得x<2-![]() ;?
;?
令f′(x)<0,解得2-![]() <x<2.?
<x<2.?
所以(-∞,2-![]() )是f(x)的增区间;?
)是f(x)的增区间;?
(2-![]() ,2)是f(x)的减区间.?
,2)是f(x)的减区间.?
(3)当2-![]() ≤0,即0<a≤
≤0,即0<a≤![]() 时,f(x)在[0,1]上是减函数,?
时,f(x)在[0,1]上是减函数,?
所以f(x)的最小值为f(1)=a.?
当0<2-![]() <1,即
<1,即![]() <a<1
<a<1![]() 时,f(x)在(0,2-)上是增函数,在(2-
时,f(x)在(0,2-)上是增函数,在(2-![]() ,1)上是减函数,?
,1)上是减函数,?
所以需比较f(0)=ln2和f(1)=a两个值的大小.?
因为![]() <2<e,所以
<2<e,所以![]() =lne<ln2<lne=1.?
=lne<ln2<lne=1.?
所以,当![]() <a<ln2时,最小值为a;当ln2≤a<1时,最小值为ln2.?
<a<ln2时,最小值为a;当ln2≤a<1时,最小值为ln2.?
当2-![]() ≥1,即a≥1时,f(x)在[0,1]上是增函数,所以最小值为f(0)=ln2.?
≥1,即a≥1时,f(x)在[0,1]上是增函数,所以最小值为f(0)=ln2.?
综上,当0<a<ln2时,f(x)的最小值为a,当a≥ln2时,f(x)的最小值为ln2.

练习册系列答案
相关题目
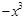 +ax在[1,+∞)上是减函数,则a的取值范围是(
)
+ax在[1,+∞)上是减函数,则a的取值范围是(
)