题目内容
在空间直角坐标系中A，B两点的坐标为A（2，3，1），B（-1，-2，-4），则A．B点之间的距离是（ ）
| A、59 | ||
B、
| ||
| C、7 | ||
| D、8 |
考点：空间两点间的距离公式
专题：空间向量及应用
分析：利用空间中两点间距离公式求解．
解答：
解：∵A（2，3，1），B（-1，-2，-4），
∴A．B点之间的距离|AB|=
=
．
故选：B．
∴A．B点之间的距离|AB|=
| (2+1)2+(3+2)2+(1+4)2 |
| 59 |
故选：B．
点评：本题考查两眯间的距离的求法，是基础题，解题时要注意空间中两点间距离公式的合理运用．
练习册系列答案
备战中考寒假系列答案
相关题目
若a=2
，b=3
，c=log32
，则（ ）
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| A、a＞b＞c |
| B、b＞a＞c |
| C、c＞a＞b |
| D、b＞c＞a |
用反证法证明某命题时，对结论：“自然数a，b，c都是偶数”，正确的反设为（ ）
| A、a，b，c中至少有一个是奇数 |
| B、a，b，c中至多有一个是奇数 |
| C、a，b，c都是奇数 |
| D、a，b，c中恰有一个是奇数 |
已知数列的前四项为1×2，2×3，3×4，4×5，则下列可以做为该数列通项的是（ ）
| A、2n |
| B、n+1 |
| C、n2+n |
| D、n2-n |
| E、n2+n |
对于实数x，“x＞6”是“x＞10”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知等比数列{an}中，a1+a2+a3=2，a2+a3+a4=4，a5+a6+a7=（ ）
| A、64 | B、32 | C、16 | D、8 |
在平面直角坐标系中，以点（1，1）为圆心，以
为半径的圆在以直角坐标系的原点为极点，以ox轴为极轴的极坐标系中对应的极坐标方程为（ ）
| 2 |
A、ρ=2
| ||||
B、ρ=2
| ||||
C、ρ=2
| ||||
D、ρ=2
|
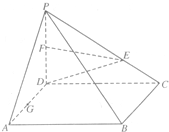如图，ABCD是正方形，PD⊥底面ABCD，点E在PC上，F，G分别是PD和AD的中点．