题目内容
已知函数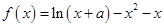 在
在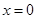 处取得极值.
处取得极值.
(1)求实数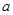 的值;
的值;
(2)若关于 的方程
的方程 在区间
在区间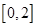 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数 的取值范围;
的取值范围;
(3)证明:对任意的正整数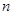 ,不等式
,不等式 都成立.
都成立.
【答案】
(1)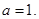 (2)
(2) 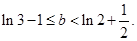 (3)先证
(3)先证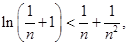
【解析】
试题分析:(1)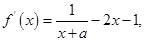
 时,
时, 取得极值,
取得极值, 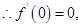
故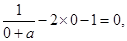 解得
解得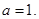 经检验
经检验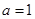 符合题意.
符合题意.
(2)由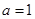 知
知 由
由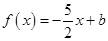 ,得
,得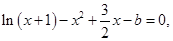
令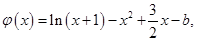 则
则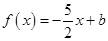 在区间
在区间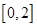 上恰有两个不同的实数根等价于
上恰有两个不同的实数根等价于 在区间
在区间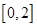 上恰有两个不同的实数根.
上恰有两个不同的实数根. 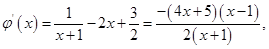
当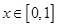 时,
时, ,于是
,于是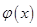 在
在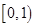 上单调递增;
上单调递增;
当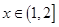 时,
时,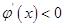 ,于是
,于是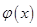 在
在 上单调递减.
上单调递减.
依题意有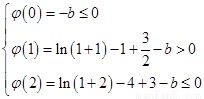 ,
,
解得,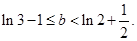
(3) 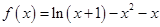 的定义域为
的定义域为 ,由(1)知
,由(1)知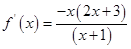 ,
,
令 得,
得,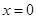 或
或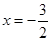 (舍去),
(舍去),  当
当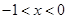 时,
时, 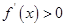 ,
, 单调递增;
单调递增;
当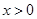 时,
时, 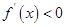 ,
, 单调递减.
单调递减. 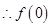 为
为 在
在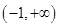 上的最大值.
上的最大值.
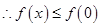 ,故
,故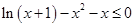 (当且仅当
(当且仅当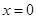 时,等号成立)
时,等号成立)
对任意正整数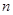 ,取
,取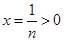 得,
得,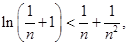
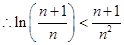
故 .
.
(方法二)数学归纳法证明:
当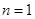 时,左边
时,左边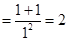 ,右边
,右边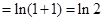 ,显然
,显然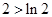 ,不等式成立.
,不等式成立.
假设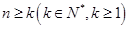 时,
时,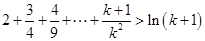 成立,
成立,
则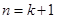 时,有
时,有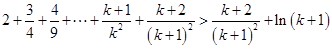 .做差比较:
.做差比较: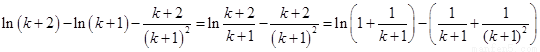
构建函数 ,则
,则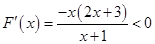 ,
,
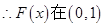 单调递减,
单调递减,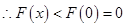 .
.
取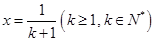 ,
,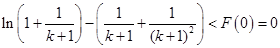
即 ,亦即
,亦即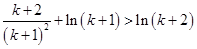 ,
,
故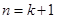 时,有
时,有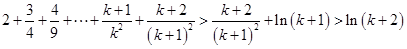 ,不等式成立.,综上可知,对任意的正整数
,不等式成立.,综上可知,对任意的正整数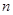 ,不等式
,不等式 都成立.
都成立.
考点:利用导数研究函数的极值函数与方程的综合运用不等式的证明.
点评:考查学生利用导数研究函数极值的能力,注意函数与方程的综合运用,以及会进行不
等式的证明.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在
在 处取得极值.
处取得极值. ;
; ,如果
,如果 在开区间
在开区间 上存在极小值,求实数
上存在极小值,求实数 的取值范围.
的取值范围. =
= 在
在 处取得极值.
处取得极值. 的值;
的值; 的方程
的方程 在
在 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围; 在
在 处取得极值。
处取得极值。 的解析式;
的解析式; 上任意两个自变量的值
上任意两个自变量的值 ,都有
,都有 ;
; 可作曲线
可作曲线 的三条切线,求实数
的三条切线,求实数 的取值范围。
的取值范围。 为实数。
为实数。 在
在 处取得极值,求
处取得极值,求 的值;
的值;
 对任意
对任意 都成立,求实数
都成立,求实数 的取值范围。
的取值范围。 在
在 处取得极值.
处取得极值. 的值;[来源:学+科+网]
的值;[来源:学+科+网] 的方程
的方程 在区间
在区间 上恰有两个不同的实数根,求实数
上恰有两个不同的实数根,求实数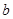 的取值范围.
的取值范围.