题目内容
四边形ABCD中,已知AB⊥AD,AB=10,BC=14,∠BAC=60°,∠D=135°,则DC=
8
| 2 |
8
.| 2 |
分析:在△ABC中,由余弦定理求得AC,再在△ACD中,由正弦定理求出DC的值.
解答:解:设AC=x,则在△ABC中,142=102+x2-2×10x×cos60°
∴x2-10x-96=0
∴x=16或x=-6(舍去)
在△ACD中,由正弦定理得:
=
∴CD=8
故答案为:8
∴x2-10x-96=0
∴x=16或x=-6(舍去)
在△ACD中,由正弦定理得:
| 16 |
| sin135° |
| CD |
| sin30° |
∴CD=8
| 2 |
故答案为:8
| 2 |
点评:本题考查正弦定理、余弦定理的应用,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
 如图四边形ABCD中,已知AC=
如图四边形ABCD中,已知AC=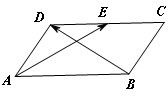 (2011•温州一模)在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,E为CD的中点,则
(2011•温州一模)在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,E为CD的中点,则