题目内容
下列四个命题中,真命题的个数为
①若函数f(x)=sinx-cosx+1,则y=|f(x)|的周期为2π;
②若函数f(x)=cos4x-sin4x,则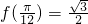 ;
;
③若角α的终边上一点P的坐标为 ,则角α的最小正值为
,则角α的最小正值为 ;
;
④函数y=2sin2x的图象可由函数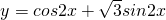 的图象向右平移
的图象向右平移 个单位得到.
个单位得到.
- A.1
- B.2
- C.3
- D.4
B
分析:①先求函数f(x)的周期,再求y=|f(x)|的周期;
②化简函数,再代入计算,即可得到结论;
③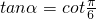 ,故角α的最小正值为
,故角α的最小正值为 ;
;
④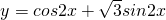 =2sin(2x+
=2sin(2x+ )=2sin[2(x+
)=2sin[2(x+ )],从而可得结论.
)],从而可得结论.
解答:①f(x)=sinx-cosx+1=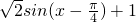 ,周期为2π,∴y=|f(x)|的周期为π,故①不正确;
,周期为2π,∴y=|f(x)|的周期为π,故①不正确;
②f(x)=cos4x-sin4x=cos2x-sin2x=cos2x,∴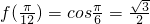 ,故②正确;
,故②正确;
③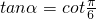 ,∴角α的最小正值为
,∴角α的最小正值为 ,故③正确;
,故③正确;
④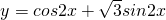 =2sin(2x+
=2sin(2x+ )=2sin[2(x+
)=2sin[2(x+ )],∴函数y=2sin2x的图象可由函数
)],∴函数y=2sin2x的图象可由函数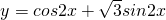 的图象向右平移
的图象向右平移 个单位得到,故④不正确
个单位得到,故④不正确
故选B.
点评:本题考查三角函数的性质,正确化简函数,利用三角函数的性质是关键.
分析:①先求函数f(x)的周期,再求y=|f(x)|的周期;
②化简函数,再代入计算,即可得到结论;
③
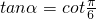 ,故角α的最小正值为
,故角α的最小正值为 ;
;④
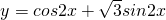 =2sin(2x+
=2sin(2x+ )=2sin[2(x+
)=2sin[2(x+ )],从而可得结论.
)],从而可得结论.解答:①f(x)=sinx-cosx+1=
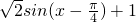 ,周期为2π,∴y=|f(x)|的周期为π,故①不正确;
,周期为2π,∴y=|f(x)|的周期为π,故①不正确;②f(x)=cos4x-sin4x=cos2x-sin2x=cos2x,∴
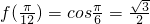 ,故②正确;
,故②正确;③
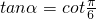 ,∴角α的最小正值为
,∴角α的最小正值为 ,故③正确;
,故③正确;④
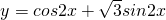 =2sin(2x+
=2sin(2x+ )=2sin[2(x+
)=2sin[2(x+ )],∴函数y=2sin2x的图象可由函数
)],∴函数y=2sin2x的图象可由函数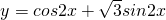 的图象向右平移
的图象向右平移 个单位得到,故④不正确
个单位得到,故④不正确故选B.
点评:本题考查三角函数的性质,正确化简函数,利用三角函数的性质是关键.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
 下列四个命题中,真命题的序号有
下列四个命题中,真命题的序号有 下列四个命题中,真命题的序号有
下列四个命题中,真命题的序号有