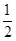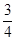题目内容
如图,矩形ABCD中,点E为边CD的中点,若在矩形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率等于( )
A. | B. | C. | D. |
C
解析试题分析:因为矩形ABCD内部随机取一个点Q,那么点Q的活动区域为矩形ABCD的面积,设长为a,宽为b,那么s=ab,而点Q取自△ABE内部时,其面积和矩形的面积关系是同底,等高,因此其面积是矩形面积的二分之一,故答案为C.
考点:本试题主要是考查了几何概型的概率的求解。
点评:解决该试题的关键是对于事件A包含的区域面积的求解,以及总的试验区间面积,然后根据面积比来求解概率。这是几何概型中常考的一个角度,面积比求解概率。同时要注意分析何为古典概型,,何为几何概型,其区别是基本事件是有穷还是无穷的问题。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
从三件正品、一件次品中随机取出两件,则取出的产品全是正品的概率是
A. | B. | C.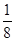 | D.无法确定 |
在棱长为 的正方体
的正方体 内任取一点
内任取一点 ,则点
,则点 到点
到点 的距离小等于
的距离小等于 的概率为
的概率为
A. | B. | C. | D. |
已知ξ~N(0,62),且P(-2≤ξ≤0)=0.4,则P(ξ>2)等于( )
| A.0.1 | B.0.2 | C.0.6 | D.0.8 |
口袋内装有大小相同的红球、白球和黑球,从中摸出一个球,摸出红球的概率是0.42,摸出白球的概率是0.28,则摸出黑球的概率是( )
| A.0.42 | B.0.28 | C.0.7 | D.0.3 |
如图,矩形长为5,宽为3,在矩形内随机撒100颗黄豆,数得落在椭圆内的黄豆数为80颗,以此实验数据为依据可以估算椭圆的面积约为( )
| A.11 | B.9 | C.12 | D.10 |