题目内容
在圆的一条直径上，任取一点作与该直径垂直的弦，则其弦长超过该圆的内接等边三角形的边长的概率为
A． | B． | C． | D． |
C
解析试题分析：
考点：本试题考查了几何概型概率的知识。
点评：解决该试题的关键是利用圆的半径以及弦长和圆心到弦中点的距离的勾股定理来得到圆内接等边三角形的边长，那么可知圆内接正三角形的边长为
，R为圆的半径，那么当弦长等于该圆的内接等边三角形的边长，则可知点在直径上的距离圆心为
的位置移动，那么可知符合题意的概率值为，故选C.
练习册系列答案
阅读快车系列答案
相关题目
在区间
上任取一个实数
，则
的概率等于
A． | B． | C． | D． |
在
上随机取一个数
，则
的概率为
A． | B． | C． | D． |
从集合
中随机取出一个数，设事件
为“取出的数是偶数”， 事件
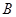为“取出的数是奇数”，则事件与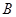
| A．是互斥且是对立事件 | B．是互斥且不对立事件 |
| C．不是互斥事件 | D．不是对立事件 |
