题目内容
口袋内装有大小相同的红球、白球和黑球,从中摸出一个球,摸出红球的概率是0.42,摸出白球的概率是0.28,则摸出黑球的概率是( )
| A.0.42 | B.0.28 | C.0.7 | D.0.3 |
D
解析试题分析:从中摸出一个球,摸出红球、摸出白球、摸出黑球是互斥的,所以由互斥事件概率的加法公式知摸出黑球的概率是1-0.42-0.28=0.3,故选D。
考点:本题主要考查互斥事件概率的加法公式。
点评:简单题,因为只摸出一个球,所以摸出红球、摸出白球、摸出黑球是互斥的。

练习册系列答案
相关题目
将一枚质地均匀的硬币连掷4次,出现“至少两次正面向上”的概率为
A. | B. | C. | D. |
在区间 上任取一个实数
上任取一个实数 ,则
,则 的概率等于
的概率等于
A. | B. | C. | D. |
从集合 中随机取出一个数,设事件
中随机取出一个数,设事件 为“取出的数是偶数”, 事件
为“取出的数是偶数”, 事件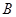 为“取出的数是奇数”,则事件
为“取出的数是奇数”,则事件 与
与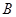
| A.是互斥且是对立事件 | B.是互斥且不对立事件 |
| C.不是互斥事件 | D.不是对立事件 |
一个均匀正方体玩具的各个面上分别标有数字1,2,3,4,5,6.将这个玩具向上抛掷1次,设事件A表示向上的一面出现奇数点,事件B表示向上的一面出现的点数不超过3,事件C表示向上的一面出现的点数不小于4,则( )
| A.A与B是互斥而非对立事件 | B.A与B是对立事件 |
| C.B与C是互斥而非对立事件 | D.B与C是对立事件 |
从五件正品,一件次品中随机取出两件,则取出的两件产品中恰好是一件正品,一件次品的概率是( )
| A.1 | B. | C. | D. |





 的分布列如下:
的分布列如下: ,则y的值为 .
,则y的值为 .