题目内容
“x2-x-6＜0”是“|x|＜2”的（ ）
| A、充要条件 |
| B、充分而不必要条件 |
| C、必要而不充分条件 |
| D、既不充分也不必要条件 |
考点：必要条件、充分条件与充要条件的判断
专题：简易逻辑
分析：根据不等式的关系结合充分条件和必要条件的定义即可得到结论．
解答：
解：由x2-x-6＜0得-2＜x＜3，
由|x|＜2得-2＜x＜2，
则“x2-x-6＜0”是“|x|＜2”的必要不充分条件，
故选：C
由|x|＜2得-2＜x＜2，
则“x2-x-6＜0”是“|x|＜2”的必要不充分条件，
故选：C
点评：本题主要考查充分条件和必要条件的判断，根据不等式的解法是解决本题的关键．
练习册系列答案
相关题目
已知a、b、c满足c＜b＜a，且ac＜0，那么下列选项中一定不成立的（ ）
| A、ab＞ac |
| B、c（b-a）＜0 |
| C、cb2≤ab2 |
| D、ac（a-c）＜0 |
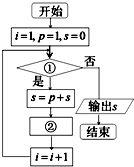给出15个数：1，2，4，7，11，…，要计算这15个数的和，现给出解决该问题的程序框图（如图所示），那么框图中判断框①处和执行框②处应分别填入（ ）| A、i≤16？；p=p+i-1 |
| B、i≤14？；p=p+i+1 |
| C、i≤15？；p=p+i+1 |
| D、i≤15？；p=p+i |
不等式
＞2的解集为（ ）
| x-1 |
| x-3 |
| A、{x|x＜1} |
| B、{x|x＞3} |
| C、{x|x＜3或x＞5} |
| D、{x|3＜x＜5} |
正项等差数列{an}中，已知a1006+a1007=4，则
+
的最小值为（ ）
| 1 |
| a1 |
| 4 |
| a2012 |
| A、9 | ||
| B、5 | ||
| C、1 | ||
D、
|
已知集合M={a，b}，N={b，c}，则M∩N=（ ）
| A、{a，b} | B、{b，c} |
| C、{a，c} | D、{b} |