题目内容
把1+（1+x）+（1+x）2+…+（1+x）n展开成关于x的多项式，其各项系数和为an，则QUOTE
等于 ．
【答案】分析：令x=1求出展开式中各项系数和，再利用极限公式求值即可求出所求．
解答：解：令x=1得an=1+2+22+…+2n=
，
．
故答案为：2
点评：本题考查二项式定理以及极限的求法，赋值法是求各项系数和的重要方法，属于中档题．
解答：解：令x=1得an=1+2+22+…+2n=
，．故答案为：2
点评：本题考查二项式定理以及极限的求法，赋值法是求各项系数和的重要方法，属于中档题．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
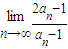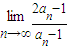等于（ ）
等于（ ）
