题目内容
 如图所示,在△ABC中,点M是BC的中点,点N在边AC上,且AN=2NC,AM与BN相交于点P,求AP:PM的值.
如图所示,在△ABC中,点M是BC的中点,点N在边AC上,且AN=2NC,AM与BN相交于点P,求AP:PM的值.
解:设 =
= ,
,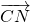 =
= ,
,
则 =
= +
+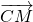 =-3
=-3 -
- ,
,
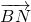 =2
=2 +
+
∵A、P、M和B、P、N分别共线,
∴存在实数λ、μ使
 =λ
=λ =-λ
=-λ -3λ
-3λ ,
, =μ
=μ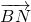 =2μ
=2μ +μ
+μ ,
,
故 =
= -
- =(λ+2μ)
=(λ+2μ) +(3λ+μ)
+(3λ+μ) .
.
而 =
= +
+ =2
=2 +3
+3
∴ 解得
解得
故 =
=
 ,即AP:PM=4:1.
,即AP:PM=4:1.
分析:根据题意把 =
= ,
,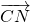 =
= ,作为该平面的一组基底,根据向量运算的三角形法则及共线向量定理分别表示出
,作为该平面的一组基底,根据向量运算的三角形法则及共线向量定理分别表示出 ,
, ,即可求得AP:PM的值.
,即可求得AP:PM的值.
点评:此题是个中档题.考查向量加法的三角形法则和共线向量定理以及平面向量基本定理,要用已知向量表示未知向量,把向量放在封闭图形中求解,体现了转化的思想和数形结合的思想方法.
 =
= ,
,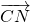 =
= ,
,则
 =
= +
+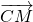 =-3
=-3 -
- ,
,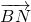 =2
=2 +
+
∵A、P、M和B、P、N分别共线,
∴存在实数λ、μ使
 =λ
=λ =-λ
=-λ -3λ
-3λ ,
, =μ
=μ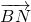 =2μ
=2μ +μ
+μ ,
,故
 =
= -
- =(λ+2μ)
=(λ+2μ) +(3λ+μ)
+(3λ+μ) .
.而
 =
= +
+ =2
=2 +3
+3
∴
 解得
解得
故
 =
=
 ,即AP:PM=4:1.
,即AP:PM=4:1.分析:根据题意把
 =
= ,
,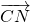 =
= ,作为该平面的一组基底,根据向量运算的三角形法则及共线向量定理分别表示出
,作为该平面的一组基底,根据向量运算的三角形法则及共线向量定理分别表示出 ,
, ,即可求得AP:PM的值.
,即可求得AP:PM的值.点评:此题是个中档题.考查向量加法的三角形法则和共线向量定理以及平面向量基本定理,要用已知向量表示未知向量,把向量放在封闭图形中求解,体现了转化的思想和数形结合的思想方法.

练习册系列答案
相关题目
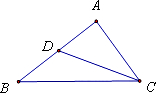 如图所示,在△ABC中,点D是边AB的中点,则向量
如图所示,在△ABC中,点D是边AB的中点,则向量| DC |
A、
| ||||||
B、
| ||||||
C、-
| ||||||
D、-
|
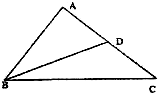 如图所示,在△ABC,已知
如图所示,在△ABC,已知 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD= 如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则
如图所示,在△ABC中,∠BAC=90°,∠ABC=60°,AD⊥BC于D,则 如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=
如图所示,在△ABC中,∠B=60°,∠C=45°,高AD=