题目内容
18.函数y=x3-2ax+a在(1,2)内有极小值,则实数a的取值范围是( )| A. | (0,$\frac{3}{2}$) | B. | (0,3) | C. | ($\frac{3}{2}$,6) | D. | (0,6) |
分析 求导,函数y=x3-2ax+a在(1,2)内有极小值,导函数在(1,2)内至少有一个实数根,从而求得实数a的取值范围.
解答 解:对于函数y=x3-2ax+a,求导可得y′=3x2-2a,
∵函数y=x3-2ax+a在(1,2)内有极小值,
∴y′=3x2-2a=0,则其有一根在(1,2)内,
a>0时,3x2-2a=0两根为±$\frac{\sqrt{6a}}{3}$,
若有一根在(1,2)内,则1<$\frac{\sqrt{6a}}{3}$<2,
即$\frac{3}{2}$<a<6,
a=0时,3x2-2a=0两根相等,均为0,f(x)在(1,2)内无极小值,
a<0时,3x2-2a=0无根,f(x)在(1,2)内无极小值,
综合可得,$\frac{3}{2}$<a<6,
故选:C.
点评 考查利用导数研究函数的极值问题,体现了转化的思想方法,属中档题.

练习册系列答案
相关题目
13.已知全集U=Z,集合A={-1,0,1},B={0,1,3},则B∩∁UA=( )
| A. | {3} | B. | {0,1} | C. | {-1} | D. | {-1,3} |
9.下列函数中x=0是极值点的函数是( )
| A. | f(x)=-x3 | B. | f(x)=x2 | C. | f(x)=sinx-x | D. | f(x)=$\frac{1}{x}$ |
7.已知{an}为等比数列,若a1+a4=8,a3+a6=2,则公比q的值为( )
| A. | ±2 | B. | $±\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
8.四个人从左到右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有( )
| A. | 12 | B. | 10 | C. | 8 | D. | 6 |
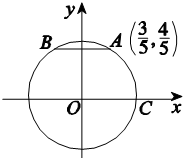 如图所示,A,B是单位圆O上的点,且B在第二象限,C是圆与x轴正半轴的交点,A点的坐标为($\frac{3}{5}$,$\frac{4}{5}$),且A与B关于y轴对称.
如图所示,A,B是单位圆O上的点,且B在第二象限,C是圆与x轴正半轴的交点,A点的坐标为($\frac{3}{5}$,$\frac{4}{5}$),且A与B关于y轴对称.