题目内容
已知{an}是各项都为正数的数列,Sn为其前n项的和,且a1=1,Sn=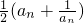 .
.
(I)分别求S22,S32的值;
(II)求数列{an}的通项an;
(III)求证:
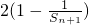 .
.
解:(I)令n=2,得1+a1= (a2+
(a2+ )?a2=
)?a2= -1(舍去负的),
-1(舍去负的),
∴s2= ?
?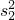 =2.
=2.
同理,令n=3可得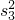 =3.
=3.
(II)∵Sn=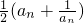 .
.
∴sn-1=sn-an= (an-
(an- ),(n≥2).
),(n≥2).
∴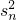 -
-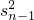 =
= (an+
(an+ )2-
)2- (an-
(an- )2=1.
)2=1.
∴{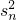 }是首项为1,公差为1的等差数列
}是首项为1,公差为1的等差数列
∴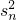 =n,
=n,
∴an=sn-sn-1= -
-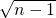 ,(n≥2).
,(n≥2).
∴an=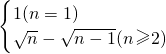 .
.
(Ⅲ)令bn=2(1-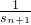 )=2(1-
)=2(1-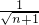 ),
),
cn=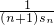 =
=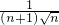 .
.
∴bn-bn-1=2(1-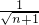 )-2(1-
)-2(1-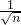 )
)
=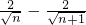 =
=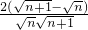
=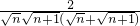
>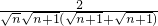 =
=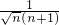 =cn.
=cn.
∴bn-bn-1>cn;
∴bn-1-bn-2>cn-1,…b2-b1>c2.
相加得:bn-b1>cn+cn-1+…+c2;
∴bn>cn+cn-1+…+c2+b1;
又∵b1=2(1- )=2-
)=2- >
> =c1.
=c1.
∴bn>cn+cn-1+…+c2+c1;
即
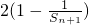 成立.
成立.
分析:(I)先把n=2代入Sn=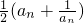 ;求出a2进而求出求S22的值;同理求出S32的值即可.
;求出a2进而求出求S22的值;同理求出S32的值即可.
(II)先根据Sn=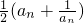 得到sn-1=sn-an=
得到sn-1=sn-an= (an-
(an- ),进而得到{
),进而得到{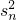 }是首项为1,公差为1的等差数列;得到{
}是首项为1,公差为1的等差数列;得到{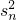 }的通项,进而求出数列{an}的通项;
}的通项,进而求出数列{an}的通项;
(III)先令bn=2(1-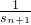 )=2(1-
)=2(1-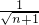 ),cn=
),cn=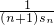 =
=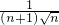 .再利用放缩法得到bn-bn-1>cn;最后求和整理即可得到结论.
.再利用放缩法得到bn-bn-1>cn;最后求和整理即可得到结论.
点评:本题主要考察数列与不等式的综合问题.解决本题的关键在于根据Sn=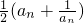 得到sn-1=sn-an=
得到sn-1=sn-an= (an-
(an- ),进而得到{
),进而得到{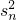 }是首项为1,公差为1的等差数列;得到{
}是首项为1,公差为1的等差数列;得到{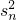 }的通项.,题后注意体会本题证明不等式的技巧及证明时构造的技巧
}的通项.,题后注意体会本题证明不等式的技巧及证明时构造的技巧
 (a2+
(a2+ )?a2=
)?a2= -1(舍去负的),
-1(舍去负的),∴s2=
 ?
?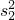 =2.
=2.同理,令n=3可得
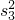 =3.
=3.(II)∵Sn=
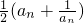 .
.∴sn-1=sn-an=
 (an-
(an- ),(n≥2).
),(n≥2).∴
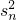 -
-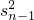 =
= (an+
(an+ )2-
)2- (an-
(an- )2=1.
)2=1.∴{
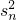 }是首项为1,公差为1的等差数列
}是首项为1,公差为1的等差数列∴
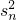 =n,
=n,∴an=sn-sn-1=
 -
-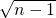 ,(n≥2).
,(n≥2).∴an=
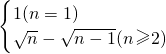 .
.(Ⅲ)令bn=2(1-
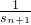 )=2(1-
)=2(1-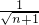 ),
),cn=
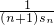 =
=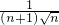 .
.∴bn-bn-1=2(1-
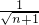 )-2(1-
)-2(1-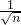 )
)=
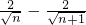 =
=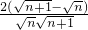
=
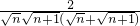
>
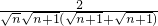 =
=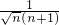 =cn.
=cn.∴bn-bn-1>cn;
∴bn-1-bn-2>cn-1,…b2-b1>c2.
相加得:bn-b1>cn+cn-1+…+c2;
∴bn>cn+cn-1+…+c2+b1;
又∵b1=2(1-
 )=2-
)=2- >
> =c1.
=c1.∴bn>cn+cn-1+…+c2+c1;
即

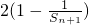 成立.
成立.分析:(I)先把n=2代入Sn=
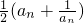 ;求出a2进而求出求S22的值;同理求出S32的值即可.
;求出a2进而求出求S22的值;同理求出S32的值即可.(II)先根据Sn=
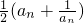 得到sn-1=sn-an=
得到sn-1=sn-an= (an-
(an- ),进而得到{
),进而得到{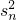 }是首项为1,公差为1的等差数列;得到{
}是首项为1,公差为1的等差数列;得到{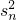 }的通项,进而求出数列{an}的通项;
}的通项,进而求出数列{an}的通项;(III)先令bn=2(1-
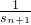 )=2(1-
)=2(1-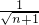 ),cn=
),cn=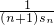 =
=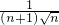 .再利用放缩法得到bn-bn-1>cn;最后求和整理即可得到结论.
.再利用放缩法得到bn-bn-1>cn;最后求和整理即可得到结论.点评:本题主要考察数列与不等式的综合问题.解决本题的关键在于根据Sn=
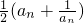 得到sn-1=sn-an=
得到sn-1=sn-an= (an-
(an- ),进而得到{
),进而得到{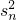 }是首项为1,公差为1的等差数列;得到{
}是首项为1,公差为1的等差数列;得到{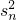 }的通项.,题后注意体会本题证明不等式的技巧及证明时构造的技巧
}的通项.,题后注意体会本题证明不等式的技巧及证明时构造的技巧 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的前n项和.
的前n项和.