题目内容

已知sinα=，sin（α+β）=，α与β均为锐角，求cos．

解：∵0＜α＜，∴cosα=．

又∵0＜α＜，0＜β＜，

∴0＜α+β＜π．若０＜α+β＜，

∵sin（α+β）＜sinα，∴α+β＜α不可能．

故＜α+β＜π．∴cos（α+β）=－．

∴cosβ=cos［（α+β）－α］

=cos（α+β）cosα+sin（α+β）sinα=－··，

∵0＜β＜，

∴0＜＜．

故cos．

练习册系列答案
相关题目
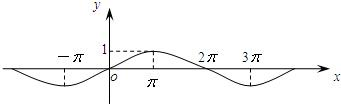精英家教网已知函数y=sinωx（ω＞0）的图象如图所示，把y=sinωx的图象向右平移
2π
3
个单位得到函数y=f（x）的图象，则f（x）=（　　）
A、sin(2x-
2π
3
)
B、sin(2x-
4π
3
)
C、sin(
1
2
x-
2π
3
)
D、sin(
1
2
x-
π
3
)
已知
cos(π-2α)
sin(α-
π
4
)
=-
2
2
，则cosα+sinα等于（　　）
A、-
7
2
B、
7
2
C、
1
2
D、-
1
2
（2013•浙江）已知α∈R，sinα+2cosα=
10
2
，则tan2α=（　　）
已知向
a
=(sin(x+
π
6
)，
3
cos(x+
π
6
))，
b
=(sin(x+
π
6
)，sin(x+
π
6
))，记f(x)=
a
•
b
，在锐角三角形ABC的三个内角A，B，C所对的边分别是a，b，c，若f（C）=1
（1）求C的大小；
（2）若c=
7
，三角形ABC的面积为
3
3
2
，求a+b的值．
（2011•延庆县一模）已知f(x)=sin(x+
π
3
)
（Ⅰ）如果sinx=
3
5
，
π
2
＜x＜π，求f（x）的值；
（Ⅱ）如果0＜x＜
π
2
，设g（x）=2f（2x），求g（x）的最大值和最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网