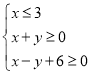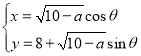题目内容
【题目】(本小题共l4分)
已知函数f(x)=![]() x +
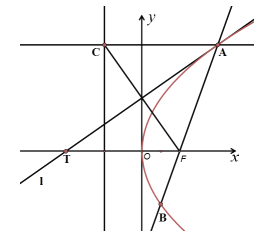
x +![]() , h(x)=
, h(x)=![]() .
.
(I)设函数F(x)=f(x)一h(x),求F(x)的单调区间与极值;
(Ⅱ)设a∈R,解关于x的方程log4[![]() ]=1og2h(a-x)一log2h (4-x);
]=1og2h(a-x)一log2h (4-x);
(Ⅲ)试比较![]() 与
与![]() 的大小.
的大小.
【答案】(Ⅰ)见解析(Ⅱ)见解析;(Ⅲ)见解析
【解析】
(Ⅰ)先求导函数,利用导函数大于0时原函数单调递增,当导函数小于0时原函数单调递减.即可求![]() 的单调区间与极值;
的单调区间与极值;
(Ⅱ)先把原等式转化为关于![]() 和
和![]() 之间的等量关系,最后利用图象来求
之间的等量关系,最后利用图象来求![]() 的值(注意对
的值(注意对![]() 的讨论).
的讨论).
(Ⅲ)把![]() 转化为一新数列
转化为一新数列![]() 的前100项和,再比较新数列
的前100项和,再比较新数列![]() 的每一项和对应
的每一项和对应![]() 之间的大小关系,即可比较
之间的大小关系,即可比较![]() 与
与![]() 的大小.
的大小.
解:(Ⅰ)由![]() 知,
知,
![]() ,令
,令![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ;
;
当![]() ,
,![]() 时,
时,![]() .
.
故![]() 时,
时,![]() 是减函数;
是减函数;
故![]() ,
,![]() 时,
时,![]() 是增函数.
是增函数.
![]() 在
在![]() 处有极小值且
处有极小值且![]() .
.
(Ⅱ)原方程可化为![]() ,
,
即![]() ,
,![]()
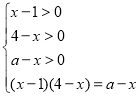
![]()
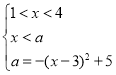
①当![]() 时,原方程有一解
时,原方程有一解![]() ;
;
②当![]() 时,原方程有两解
时,原方程有两解![]() ;
;
③当![]() 时,原方程有一解
时,原方程有一解![]() ;
;
④当![]() 或
或![]() 时,原方程无解.
时,原方程无解.
(Ⅲ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
从而有![]() .
.
当![]() 时,
时,
![]() ,
,![]()
![]()
![]()
![]() .
.
即对任意的![]() ,都有
,都有![]() .
.
又因为![]() ,
,
所以![]() (1)
(1)![]() (2)
(2)![]() .
.
故![]() .
.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目