题目内容
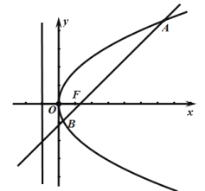
【题目】已知椭圆![]() :
:![]() 和圆
和圆![]() :
:![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上,当直线
上,当直线![]() 与圆
与圆![]() 相切时,
相切时,![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,且与椭圆
,且与椭圆![]() 和圆
和圆![]() 都相切,切点分别为
都相切,切点分别为![]() ,
,![]() ,记
,记![]() 和
和![]() 的积分别为
的积分别为![]() 和
和![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(I) 由题意可得![]() ,设
,设![]() ,运用直线和圆相切的条件,可得
,运用直线和圆相切的条件,可得![]() ,结合a,b, c的关系,解得a, c,进而得到椭圆方程;
,结合a,b, c的关系,解得a, c,进而得到椭圆方程;
(Ⅱ)设![]() ,
,![]() ,将
,将![]() 代入
代入![]() ,结合直线和椭圆相切的条件判别式为0,解得M的坐标,可得
,结合直线和椭圆相切的条件判别式为0,解得M的坐标,可得![]() 的面积
的面积![]() ,再由直线和圆相切的条件,解方程可得N的坐标,求得Q的坐标,计算
,再由直线和圆相切的条件,解方程可得N的坐标,求得Q的坐标,计算![]() 的面积为
的面积为![]() ,求得
,求得![]() 的表达式,化简后运用基本不等式即可得证.
的表达式,化简后运用基本不等式即可得证.
(Ⅰ)由题可知![]() . ①
. ①
设![]() ,则由
,则由![]() 与圆相切时
与圆相切时![]() 得
得![]() ,即
,即![]() . ②
. ②
将①②代入![]() 解得
解得![]() .
.
所以![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,
将![]() 代入
代入![]() 得
得![]() ,
,
由直线![]() 与椭圆
与椭圆![]() 相切得
相切得![]() 即
即![]() ,且
,且
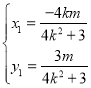 ,
,
则![]() 的面积
的面积![]() .
.
由直线![]() 与圆
与圆![]() 相切,设
相切,设![]() :
:![]() ,与
,与![]() 联立得
联立得
 .
.
直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,则
,则![]() .
.
则![]() 的面积
的面积![]() ,
,
从而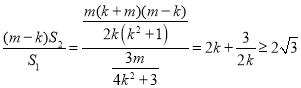 .(当且仅当
.(当且仅当![]() 时等号成立),
时等号成立),
所以![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
相关题目
【题目】某工厂新购置甲、乙两种设备,分别生产A,B两种产品,为了解这两种产品的质量,随机抽取了200件进行质量检测,得到质量指标值的频数统计表如下:
质量指标值 |
|
|
|
|
|
| 合计 |
A产品频数 | 2 | 6 | a | 32 | 20 | 10 | 80 |
B产品频数 | 12 | 24 | b | 27 | 15 | 6 | n |
产品质量2×2列联表
产品质量高 | 产品质量一般 | 合计 | |
A产品 | |||
B产品 | |||
合计 |
附: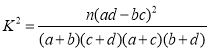
|
|
|
|
|
|
|
|
(1)求a,b,n的值,并估计A产品质量指标值的平均数;
(2)若质量指标值大于50,则说明该产品质量高,否则说明该产品质量一般.请根据频数表完成![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为质量高低与引入甲、乙设备有关.
的把握认为质量高低与引入甲、乙设备有关.