题目内容
【题目】已知线段![]() 是过抛物线
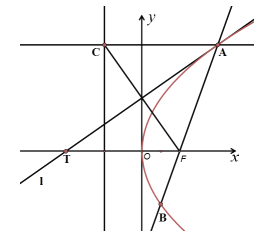
是过抛物线![]() 的焦点F的一条弦,过点A(A在第一象限内)作直线
的焦点F的一条弦,过点A(A在第一象限内)作直线![]() 垂直于抛物线的准线,垂足为C,直线
垂直于抛物线的准线,垂足为C,直线![]() 与抛物线相切于点A,交x轴于点T,给出下列命题:
与抛物线相切于点A,交x轴于点T,给出下列命题:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() .
.
其中正确的命题个数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
根据抛物线的定义得到![]() ,然后判断出过
,然后判断出过![]() 点的抛物线的切线垂直
点的抛物线的切线垂直![]() ,进而判断出三个命题正确.
,进而判断出三个命题正确.
根据抛物线的定义可知![]() ,由于
,由于![]() 垂直抛物线的准线,所以
垂直抛物线的准线,所以![]() 轴,
轴,
所以![]() .
.
设 ,则
,则![]() ,设
,设![]() 是
是![]() 的中点,
的中点,
则![]() .
.
所以直线![]() 的方程为
的方程为 ,
,
即![]() .
.
由 消去
消去![]() 并化简得
并化简得![]() ,
,
其判别式![]() ,
,
所以直线![]() 与抛物线相切,故直线
与抛物线相切,故直线![]() 与直线
与直线![]() 重合.
重合.
由于![]() 是
是![]() 的中点,所以
的中点,所以![]() ,也即
,也即![]() ,命题(3)成立.
,命题(3)成立.
根据等腰三角形的性质可知![]() ,
,
所以![]() ,命题(1)成立.
,命题(1)成立.
由于![]() 轴,所以
轴,所以![]() ,
,
所以![]() ,所以
,所以![]() ,命题(2)成立.
,命题(2)成立.
综上所述,正确的命题个数为![]() 个.
个.
故选:D

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国委员会第二次会议,分别于2019年3月5日和3月3日在北京召开为了了解哪些人更关注“两会”,某机构随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制的频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”经统计“青少年人”和“中老年人”的人数之比为
内的人分别称为“青少年人”和“中老年人”经统计“青少年人”和“中老年人”的人数之比为![]() .其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是
.其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是![]() .
.

(1)求图中![]() 的值;现釆用分层抽样在
的值;现釆用分层抽样在![]() 和
和![]() 中随机抽取8名代表,从8人中仼选2人,求2人中至少有1个是“中老年人”的概率是多少?
中随机抽取8名代表,从8人中仼选2人,求2人中至少有1个是“中老年人”的概率是多少?
(2)根据已知条件,完成下面的![]() 列联表,并根据此统计结果判断:能否有
列联表,并根据此统计结果判断:能否有![]() 的把握认为“中老年人”比“青少年人”更加关注“两会”?
的把握认为“中老年人”比“青少年人”更加关注“两会”?
关注 | 不关注 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
参考数据及公式:
| 0.150 | 0.100 | 0.050 | 0.010 | 0.001 |
| 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |