题目内容
已知 ,
, 是两个不共线的单位向量,向量
是两个不共线的单位向量,向量 =3
=3 -
- ,
, =t
=t +2
+2 ,且
,且 ∥
∥ ,则t=
,则t=
- A.-6
- B.6
- C.-3
- D.3
A
分析:由于已知 =3
=3 -
- ,
, =t
=t +2
+2 ,由题意可得,必存在一个实数λ,使得
,由题意可得,必存在一个实数λ,使得 ,由此等式得到t的方程求出k的值,即可选出正确选项
,由此等式得到t的方程求出k的值,即可选出正确选项
解答:由题意,故必存在一个实数λ,使得 ,
,
∴ =
=
∴
解得t=-6
故选A
点评:本题考查向量共线定理,利用向量共线定理建立关于参数t的方程,向量共线定理的考查是高考热点,此类题难度较低,属于基础题
分析:由于已知
 =3
=3 -
- ,
, =t
=t +2
+2 ,由题意可得,必存在一个实数λ,使得
,由题意可得,必存在一个实数λ,使得 ,由此等式得到t的方程求出k的值,即可选出正确选项
,由此等式得到t的方程求出k的值,即可选出正确选项解答:由题意,故必存在一个实数λ,使得
 ,
,∴
 =
=
∴

解得t=-6
故选A
点评:本题考查向量共线定理,利用向量共线定理建立关于参数t的方程,向量共线定理的考查是高考热点,此类题难度较低,属于基础题

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 已知
已知 、
、 是两个不共线的向量,O是同一平面内的一个定点,
是两个不共线的向量,O是同一平面内的一个定点, ,则以下结论中,错误的是
,则以下结论中,错误的是 .
.
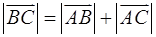 .
D.以上选项A、B、C不全对
.
D.以上选项A、B、C不全对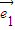 ,
,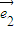 是两个不共线的单位向量,向量
是两个不共线的单位向量,向量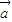 =3
=3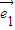 -
-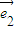 ,
, =t
=t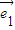 +2
+2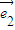 ,且
,且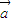 ∥
∥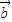 ,则t=( )
,则t=( )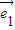 、
、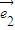 是两个不共线的平面向量,向量
是两个不共线的平面向量,向量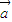 =2
=2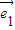 -
-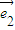 ,
,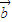 =
=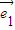 +λ
+λ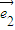 (λ∈R),若
(λ∈R),若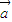 ∥
∥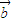 ,则λ= .
,则λ= .