题目内容
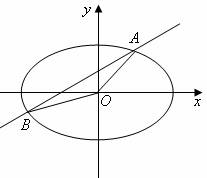
如图,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,记
两点,记![]() 的面积为
的面积为![]() .
.
(I)求在![]() ,
,![]() 的条件下,
的条件下,![]() 的最大值;
的最大值;
(II)当![]() ,
,![]() 时,求直线
时,求直线![]() 的方程.
的方程.

(Ⅰ)解:设点![]() 的坐标为
的坐标为![]() ,
,
点![]() 的坐标为
的坐标为![]() ,………1分
,………1分
由![]() ,代入方程:
,代入方程:
解得![]() ,…………… 3分
,…………… 3分
所以![]()
![]()
![]() .(基本不等式)
.(基本不等式)
…………… 5分
当且仅当![]() 时,
时,![]() 取到最大值
取到最大值![]() .……………6分
.……………6分
(II)当![]() ,
,![]() 时,求直线
时,求直线![]() 的方程.
的方程.
(Ⅱ)解:由
得![]() ,
,
![]() ,……… 8分 ①
,……… 8分 ①
![]()
 . …… 9分 ②
. …… 9分 ②
设![]() 到
到![]() 的距离为
的距离为![]() ,
,
则![]() ,…………… 10分
,…………… 10分![]()
又因为![]() ,
,
所以![]() ,代入②式并整理,得
,代入②式并整理,得
![]() ,
, ![]() …………… 12分
…………… 12分
解得![]() ,
,![]() ,
,
代入①式检验,![]() ,均符合题意
,均符合题意
…………… 13分
故直线![]() 的方程是
的方程是
![]() 或
或![]()
或![]() ,或
,或![]() …………… 14分
…………… 14分

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目

 如图,直线
如图,直线
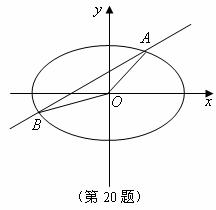
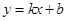 与椭圆
与椭圆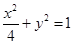 交于
交于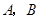 两点,记
两点,记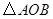 的面积为
的面积为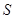 .
.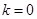 ,
,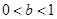 的条件下,
的条件下,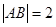 ,
,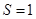 时,求直线
时,求直线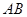 的方程.
的方程.