��Ŀ����
��ͼ����֪��Բ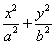 ��1(a��b��0)��������Ϊ
��1(a��b��0)��������Ϊ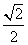 ���Ը���Բ�ϵĵ����Բ�����ҽ���F1��F2Ϊ����������ε��ܳ�Ϊ4(
���Ը���Բ�ϵĵ����Բ�����ҽ���F1��F2Ϊ����������ε��ܳ�Ϊ4(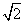 ��1)��һ����˫���ߵĶ����Ǹ���Բ�Ľ��㣬��PΪ��˫���������ڶ������һ�㣬ֱ��PF1��PF2����Բ�Ľ���ֱ�ΪA��B��C��D.
��1)��һ����˫���ߵĶ����Ǹ���Բ�Ľ��㣬��PΪ��˫���������ڶ������һ�㣬ֱ��PF1��PF2����Բ�Ľ���ֱ�ΪA��B��C��D.
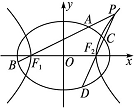
(1)����Բ��˫���ߵı����̣�
(2)��ֱ��PF1��PF2��б�ʷֱ�Ϊk1��k2��֤����k1��k2��1��
(3)�Ƿ���ڳ����ˣ�ʹ��|AB|��|CD|����|AB|��|CD|������������ڣ���˵�ֵ���������ڣ���˵�����ɣ�
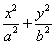 ��1(a��b��0)��������Ϊ
��1(a��b��0)��������Ϊ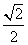 ���Ը���Բ�ϵĵ����Բ�����ҽ���F1��F2Ϊ����������ε��ܳ�Ϊ4(
���Ը���Բ�ϵĵ����Բ�����ҽ���F1��F2Ϊ����������ε��ܳ�Ϊ4(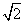 ��1)��һ����˫���ߵĶ����Ǹ���Բ�Ľ��㣬��PΪ��˫���������ڶ������һ�㣬ֱ��PF1��PF2����Բ�Ľ���ֱ�ΪA��B��C��D.
��1)��һ����˫���ߵĶ����Ǹ���Բ�Ľ��㣬��PΪ��˫���������ڶ������һ�㣬ֱ��PF1��PF2����Բ�Ľ���ֱ�ΪA��B��C��D. 
(1)����Բ��˫���ߵı����̣�
(2)��ֱ��PF1��PF2��б�ʷֱ�Ϊk1��k2��֤����k1��k2��1��
(3)�Ƿ���ڳ����ˣ�ʹ��|AB|��|CD|����|AB|��|CD|������������ڣ���˵�ֵ���������ڣ���˵�����ɣ�
(1)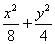 ��1.
��1.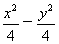 ��1.(2)��A(x1��y1)��B(x2��y2)��P(x0��y0)��
��1.(2)��A(x1��y1)��B(x2��y2)��P(x0��y0)��
��k1��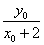 ��k2��
��k2��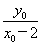 .��Ϊ��P��˫����x2��y2��4�ϣ�����x��y��4.
.��Ϊ��P��˫����x2��y2��4�ϣ�����x��y��4.
���k1��k2��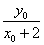 ��
��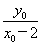 ��
��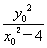 ��1����k1��k2��1.
��1����k1��k2��1.
(3)���ڦˣ�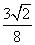 ��ʹ|AB|��|CD|����|AB|��|CD|�������
��ʹ|AB|��|CD|����|AB|��|CD|�������
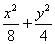 ��1.
��1.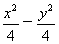 ��1.(2)��A(x1��y1)��B(x2��y2)��P(x0��y0)��
��1.(2)��A(x1��y1)��B(x2��y2)��P(x0��y0)����k1��
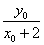 ��k2��
��k2��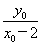 .��Ϊ��P��˫����x2��y2��4�ϣ�����x��y��4.
.��Ϊ��P��˫����x2��y2��4�ϣ�����x��y��4.���k1��k2��
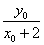 ��
��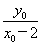 ��
��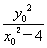 ��1����k1��k2��1.
��1����k1��k2��1.(3)���ڦˣ�
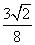 ��ʹ|AB|��|CD|����|AB|��|CD|�������
��ʹ|AB|��|CD|����|AB|��|CD|����������������(1)����Բ�İ뽹��Ϊc��������֪��
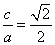 ��
�� 2a��2c��4(
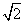 ��1)������a��2
��1)������a��2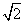 ��c��2.
��c��2.��a2��b2��c2�����b��2.����Բ�ı�����Ϊ
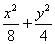 ��1.
��1.�����������˫���ߵı�����Ϊ
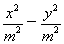 ��1(m��0)����Ϊ����˫���ߵĶ�������Բ�Ľ��㣬����m��2�����˫���ߵı�����Ϊ
��1(m��0)����Ϊ����˫���ߵĶ�������Բ�Ľ��㣬����m��2�����˫���ߵı�����Ϊ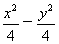 ��1.
��1.(2)��A(x1��y1)��B(x2��y2)��P(x0��y0)����k1��
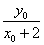 ��k2��
��k2��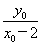 .
.��Ϊ��P��˫����x2��y2��4�ϣ�����x��y��4.
���k1��k2��
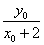 ��
��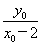 ��
��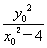 ��1����k1��k2��1.
��1����k1��k2��1.(3)����PF1�ķ���Ϊy��k1(x��2)�����������Բ���̵�(2k
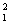 ��1)x2��8k
��1)x2��8k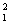 x��8k
x��8k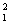 ��8��0��
��8��0����Ȼ2k
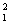 ��1��0����Ȼ����0.��Τ�ﶨ����x1��x2��
��1��0����Ȼ����0.��Τ�ﶨ����x1��x2��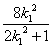 ��x1x2��
��x1x2��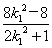 .
.����|AB|��
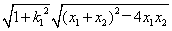
��
 .
.ͬ���ɵ�|CD|��
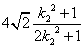 .
.��
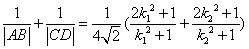 ��
����k1��k2��1��
����
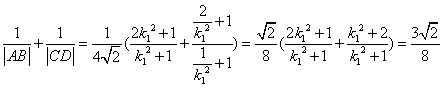 .
.��|AB|��|CD|��
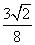 |AB|��|CD|.
|AB|��|CD|.��˴��ڦˣ�
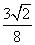 ��ʹ|AB|��|CD|����|AB|��|CD|�������
��ʹ|AB|��|CD|����|AB|��|CD|�����������������ֱ����Բ���ߵ��ۺ����⣬����Ҫ�������̣�ͬʱ���һԪ���η��̸���ϵ���Ĺ�ϵ������⣻��������ֵ���⣬��ɽ��ñ���ʽ��ֱ��б��k��ʾ��Ȼ��������⽫����л����ϱ���ʽ����ʽѡȡ��ֵ�ļ��㷽ʽ

��ϰ��ϵ�д�
�����Ŀ
 �У�˫����������ԭ�㣬������
�У�˫����������ԭ�㣬������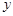 ���ϣ�һ�������߷���Ϊ
���ϣ�һ�������߷���Ϊ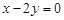 ��
��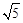
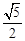
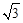
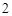
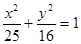 �ϵ�һ��P������Բһ������ľ���Ϊ������P����һ�������Ϊ�� ��
�ϵ�һ��P������Բһ������ľ���Ϊ������P����һ�������Ϊ�� ��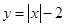 ��ͼ��������
��ͼ��������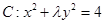 ǡ����������ͬ�Ĺ����㣬��ʵ��
ǡ����������ͬ�Ĺ����㣬��ʵ��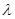 ��ȡֵ��Χ��
��ȡֵ��Χ��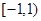
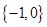
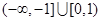
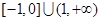
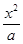 +
+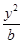 =1(
=1(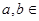 {1��2��3��4������2013})�������У�����Բ����ĺ͵��� ����������С����Բ����Ϊ .
{1��2��3��4������2013})�������У�����Բ����ĺ͵��� ����������С����Բ����Ϊ .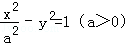 �����ĺ��㣬��PΪ˫������֧�ϵ�����һ�㣬��
�����ĺ��㣬��PΪ˫������֧�ϵ�����һ�㣬��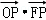 ��ȡֵ��ΧΪ
��ȡֵ��ΧΪ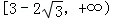
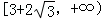
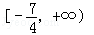
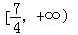
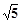 ��������e=
��������e=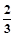 ����Բ��������ΪF1��F2����F1��ֱ�߽���Բ��A��B���㣬���ABF2�ܳ�Ϊ_____________��
����Բ��������ΪF1��F2����F1��ֱ�߽���Բ��A��B���㣬���ABF2�ܳ�Ϊ_____________��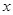 �ᣬ��ʵ�᳤Ϊ2��������
�ᣬ��ʵ�᳤Ϊ2��������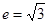 , L�ǹ�����
, L�ǹ�����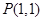 ��ֱ��.
��ֱ��.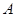 ,
,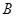 ���㣬���߶�
���㣬���߶�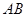 ǡ���Ե�
ǡ���Ե�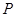 Ϊ�е㣬�����ڣ����ֱ��L�ķ��̣������棬˵������.
Ϊ�е㣬�����ڣ����ֱ��L�ķ��̣������棬˵������.