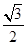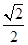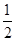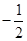题目内容
在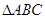 中,满足
中,满足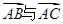 的夹角为
的夹角为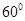 ,
,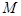 是
是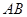 的中点,
的中点,
(1)若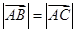 ,求向量
,求向量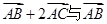 的夹角的余弦值;.
的夹角的余弦值;.
(2)若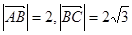 ,点
,点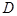 在边
在边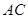 上且
上且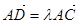 ,如果
,如果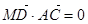 ,求
,求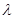 的值。
的值。
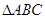 中,满足
中,满足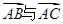 的夹角为
的夹角为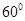 ,
,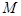 是
是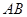 的中点,
的中点, (1)若
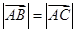 ,求向量
,求向量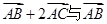 的夹角的余弦值;.
的夹角的余弦值;.(2)若
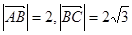 ,点
,点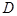 在边
在边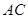 上且
上且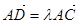 ,如果
,如果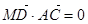 ,求
,求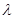 的值。
的值。(1) ;(2)
;(2) ,
,
 ;(2)
;(2) ,
,试题分析:(1)本小题考查平面向量的基本运算,利用
 来求两个向量的夹角的余弦值;
来求两个向量的夹角的余弦值;(2)本小题首先利用余弦定理建立边角关系
 ,然后求解
,然后求解 ,代入化简可得
,代入化简可得 .
.试题解析:(1)设
 ,则
,则 , 3分
, 3分而
 , 5分
, 5分所以向量
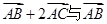 的夹角的余弦值等于
的夹角的余弦值等于 。 8分
。 8分(2)在
 解得
解得 , 10分
, 10分因为
 ,所以
,所以 , 12分
, 12分故
 。 14分
。 14分
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
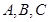 所对的边长分别为
所对的边长分别为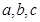 ,
,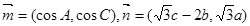 ,且
,且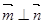 .
.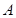 的大小;
的大小;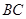 边上的中线
边上的中线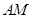 的长为
的长为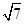 ,求
,求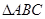 的面积.
的面积.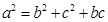 .
.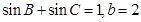 ,试求△ABC的面积.
,试求△ABC的面积. ,函数
,函数 .
. 的最值和单调递减区间;
的最值和单调递减区间; ,
, ,求△ABC的面积的最大值.
,求△ABC的面积的最大值.
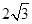
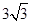
 中,若
中,若 ,
, ,
, ,则
,则 .
. 、
、 、
、 分别为△
分别为△ 的三个内角
的三个内角 、
、 、
、 所对的边,若
所对的边,若 ,
, ,
, ,则边
,则边 ;
; 中,角
中,角 所对边的长分别为
所对边的长分别为 ,若
,若 ,则
,则 的最小值为( )
的最小值为( )



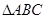 中,角
中,角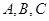 所对边长分别为
所对边长分别为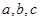 ,若
,若 ,则
,则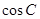 的最小值为( )
的最小值为( )