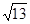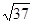题目内容
设三角形ABC的内角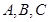 所对的边长分别为
所对的边长分别为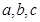 ,
,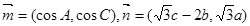 ,且
,且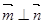 .
.
(Ⅰ)求角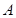 的大小;
的大小;
(Ⅱ)若AC=BC,且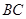 边上的中线
边上的中线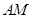 的长为
的长为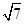 ,求
,求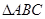 的面积.
的面积.
 所对的边长分别为
所对的边长分别为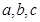 ,
,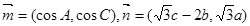 ,且
,且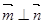 .
.(Ⅰ)求角
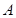 的大小;
的大小;(Ⅱ)若AC=BC,且
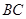 边上的中线
边上的中线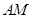 的长为
的长为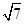 ,求
,求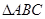 的面积.
的面积.(Ⅰ)A=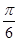 ;(Ⅱ)
;(Ⅱ)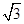
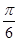 ;(Ⅱ)
;(Ⅱ)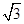
试题分析:(Ⅰ)由
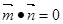 可得
可得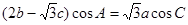 通过三角运算即sin(A+C)=sinB.可求得角A的值.
通过三角运算即sin(A+C)=sinB.可求得角A的值.(Ⅱ)由角A=
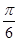 .可求得C=
.可求得C=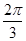 .又因为AC=2CM.即AM=
.又因为AC=2CM.即AM= 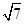 .在三角形AMC中可求得AC的长.再用三角形面积公式即可求得三角形的面积.本题是利用向量垂直知识来求得角A.再根据等腰三角形的内角关系,利用余弦定理求得三角形的面积.
.在三角形AMC中可求得AC的长.再用三角形面积公式即可求得三角形的面积.本题是利用向量垂直知识来求得角A.再根据等腰三角形的内角关系,利用余弦定理求得三角形的面积.试题解析:(1)由
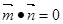
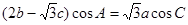 1分
1分所以
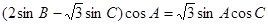 2分
2分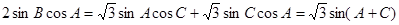
则2sinBcosA=
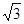 sinB 4分
sinB 4分所以cosA=
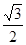 于是A=
于是A=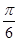 6分
6分(2)由(1)知A=
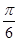 ,又AC=BC,所以C=
,又AC=BC,所以C=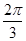 7分
7分设AC=x,则MC=
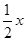 ,AM=
,AM=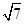 ,在
,在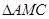 中,由余弦定理得
中,由余弦定理得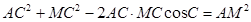 9分
9分即
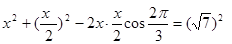
解得x=2 11分
故
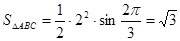 13分
13分
练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
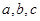 分别为角
分别为角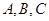 所对的三边,已知
所对的三边,已知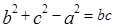
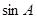 的值
的值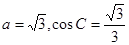 ,求边
,求边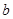 的长.
的长. 两个小岛相距10
两个小岛相距10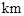 ,船O将保持观望A岛和B岛所成的视角为
,船O将保持观望A岛和B岛所成的视角为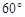 ,现从船O上派下一只小艇沿
,现从船O上派下一只小艇沿 方向驶至
方向驶至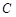 处进行作业,且
处进行作业,且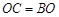 .设
.设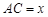

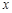 分别表示
分别表示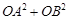 和
和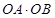 ,并求出
,并求出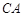 的距离为
的距离为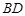 ,求BD的最大值.
,求BD的最大值.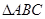 中,设内角
中,设内角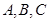 的对边分别为
的对边分别为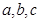 ,向量
,向量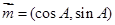 ,向量
,向量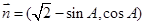 ,若
,若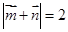
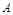 的大小;
的大小;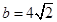 ,且
,且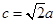 ,求
,求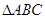 中,满足
中,满足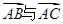 的夹角为
的夹角为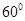 ,
,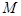 是
是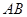 的中点,
的中点, 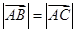 ,求向量
,求向量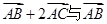 的夹角的余弦值;.
的夹角的余弦值;.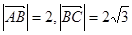 ,点
,点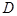 在边
在边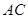 上且
上且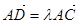 ,如果
,如果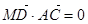 ,求
,求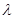 的值。
的值。 中,若角
中,若角 所对的三边
所对的三边 成等差数列,则下列结论中正确的是____________.
成等差数列,则下列结论中正确的是____________. ; ③
; ③ ; ④
; ④ ;
;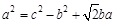 ,则∠C=( )
,则∠C=( )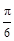
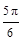

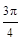
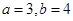 ,∠C=
,∠C=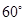 , 则边 c 的值等于( )
, 则边 c 的值等于( )