题目内容
已知方程x2sinθ+y2=sin2θ表示焦点在y轴上的双曲线,则点P(cosθ,sinθ)在
- A.第一象限
- B.第二象限
- C.第三象限
- D.第四象限
C
分析:将双曲线化成焦点在y轴上的双曲线的标准形式: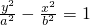 ,可得a2=sin2θ>0,b2=
,可得a2=sin2θ>0,b2= >0,再结合二倍角的正弦公式,得到sinθ<0且cosθ<0,因此得到P(cosθ,sinθ)第三象限,可得正确选项.
>0,再结合二倍角的正弦公式,得到sinθ<0且cosθ<0,因此得到P(cosθ,sinθ)第三象限,可得正确选项.
解答:∵方程x2sinθ+y2=sin2θ表示焦点在y轴上的双曲线
∴原方程化为标准形式:
∵sin2θ=2sinθcosθ
∴原方程的标准形式可化简为:
∴ ?
?
∴sinθ<0且cosθ<0,
因此P(cosθ,sinθ)第三象限
故选C
点评:本题借助于双曲线的标准方程为载体,着重考查了双曲线的基本概念、三角函数的符号和二倍角的三角函数公式,属于基础题.
分析:将双曲线化成焦点在y轴上的双曲线的标准形式:
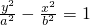 ,可得a2=sin2θ>0,b2=
,可得a2=sin2θ>0,b2= >0,再结合二倍角的正弦公式,得到sinθ<0且cosθ<0,因此得到P(cosθ,sinθ)第三象限,可得正确选项.
>0,再结合二倍角的正弦公式,得到sinθ<0且cosθ<0,因此得到P(cosθ,sinθ)第三象限,可得正确选项.解答:∵方程x2sinθ+y2=sin2θ表示焦点在y轴上的双曲线
∴原方程化为标准形式:

∵sin2θ=2sinθcosθ
∴原方程的标准形式可化简为:

∴
 ?
?
∴sinθ<0且cosθ<0,
因此P(cosθ,sinθ)第三象限
故选C
点评:本题借助于双曲线的标准方程为载体,着重考查了双曲线的基本概念、三角函数的符号和二倍角的三角函数公式,属于基础题.

练习册系列答案
相关题目
已知α∈(0,
),方程x2sinα+y2cosα=1表示焦点在y轴上的椭圆,则α的取值范围是( )
| π |
| 2 |
A、(0,
| ||||
B、(0,
| ||||
C、[
| ||||
D、(
|