题目内容
(12分)函数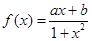 是定义域在(-1,1)上奇函数,且
是定义域在(-1,1)上奇函数,且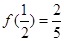 .
.
(1)确定函数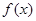 的解析式;
的解析式;
(2)用定义证明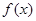 在(-1,1)上是增函数;
在(-1,1)上是增函数;
(3)解不等式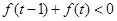 .
.
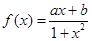 是定义域在(-1,1)上奇函数,且
是定义域在(-1,1)上奇函数,且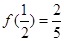 .
.(1)确定函数
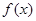 的解析式;
的解析式;(2)用定义证明
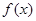 在(-1,1)上是增函数;
在(-1,1)上是增函数;(3)解不等式
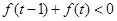 .
.(1)
 (2)
(2) 

即


(2)证明:任取
 ,
, 则
 =
= .
.∵
 ,∴
,∴
 ∴
∴
∴
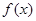 在(-1,1)上是增函数.
在(-1,1)上是增函数.(3)

∵
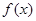 在(-1,1)上是增函数
在(-1,1)上是增函数∴
 ,解得
,解得 .
.点评:(1)单调性的证明过程中注意一定要化为能够清楚判断正负的乘积形式(2)应用单调性解不等式注意函数的定义域。

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
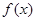 的定义域为
的定义域为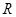 ,对于任意的
,对于任意的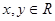 ,都有
,都有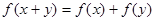 ,且当
,且当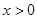 时,
时,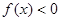 ,若
,若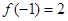 .
.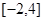 上的值域.
上的值域. ,则函数
,则函数 的值域是( )
的值域是( )



 的定义域为 .
的定义域为 . 在区间
在区间 上是增函数,若
上是增函数,若 ,则实数
,则实数 的取值范围是____________.
的取值范围是____________. 的定义域为 .
的定义域为 . 的值域为
的值域为 则其定义域是( )
则其定义域是( )



 的定义域;
的定义域; 的值域;
的值域; 的定义域为( )
的定义域为( )


