Question

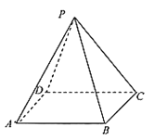
【题目】如图，四棱锥中，四边形是边长为2的菱形，

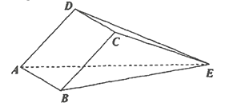
（1）证明：平面平面；

（2）当平面与平面所成锐二面角的余弦值，求直线与平面所成角正弦值.

Answer 1

【答案】（1）见解析（2）

【解析】

（1）过D作，垂直为O，连接，利用勾股定理证得，结合，证得平面，即可得到平面平面；

（2）建立空间直角坐标系，求出两平面的法向量，通过计算法向量的夹角的余弦值，求得的长，再结合线面角的定义，即可求解.

（1）过D作，垂直为O，连接，

在中，，，可得，

在中，

由余弦定理可得，

所以，

因为，所以为等边三角形，所以，

所以，可得，又由，且，

所以平面，又平面，所以平面平面.

（2）由（1）知，以O为原点，，，方向分别为x，y，z轴正方向，建立空间直角坐标系

设，则，，，，

所以，

设平面的法向量为，则，即

令，，

平面的法向量为，

由，解得

因为平面，所以为与平面所成的角，所以，

即直线与平面所成角正弦值.