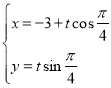题目内容
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的单调性和极值;
的单调性和极值;
(Ⅱ)若函数![]() 至少有1个零点,求
至少有1个零点,求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,极小值为-2,无极大值 (Ⅱ)
上单调递增,极小值为-2,无极大值 (Ⅱ)![]()
【解析】
(Ⅰ)求导得到![]() ,分别得到当
,分别得到当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,判断出
,判断出![]() 单调性,从而得到其极值;
单调性,从而得到其极值;
(Ⅱ)根据题意得到![]() ,令
,令![]() ,求导得到
,求导得到![]() ,由
,由![]() 得
得![]() ,令
,令![]() ,由零点存在定理得到存在
,由零点存在定理得到存在![]() ,使得
,使得![]() ,由
,由![]() 得到
得到![]() 的最小值,再对
的最小值,再对![]() 的零点进行分类讨论,得到答案.
的零点进行分类讨论,得到答案.
(Ⅰ)当![]() 时,
时,![]() ,
,
∴![]()
当![]() 时,
时,![]() ,
,![]() ,
,
∴![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
∴![]()
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
![]() 在
在![]() 处取得极小值,极小值为
处取得极小值,极小值为![]() ,无极大值
,无极大值
(Ⅱ)∵![]() ,
,
由![]() 得
得![]()
令![]() ,
,
则![]()
由![]() 得
得![]() .
.
令![]() ,当
,当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 单调递增,
单调递增,
∵![]() ,
,![]() ,
,
∴存在![]() ,使得
,使得![]()
且当![]() 时,
时,![]() ,即
,即![]() ,
,
当![]() 时,
时,![]() ,即
,即![]()
∵![]() ,
,![]() ,
,
∴当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
∴![]() 在
在![]() 处取得最小值
处取得最小值![]()
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,即
,即![]()
∴当![]() 时,函数
时,函数![]() 无零点,
无零点,
当![]() 时,∵
时,∵![]() ,
,
∴函数![]() 至少有1个零点,
至少有1个零点,
故![]() 的取值范围是
的取值范围是![]() .
.

【题目】为了促进我国人口均衡发展,从2016年1月1日起,全国统一实施全面放开二孩政策,这也是为了重建大国人口观,重新认识人口价值、人口规律、人口问题,某研究机构为了了解人们对全面放开生育二孩政策的态度,随机调查了200人,得到的统计数据如下面的不完整的2×2列联表所示(单位:人):
支持生育二孩 | 不支持生育二孩 | 合计 | |
男性 | 30 | ||
女性 | 60 | 100 | |
合计 | 70 |
(1)完成2×2列联表,并求是否有90%的把握认为是否“支持生育二孩”与性别有关?
(2)现从样本中的女性中利用分层抽样的方法抽取5人,再从这5人中随机选出2人进行深层次的交流,求选出的2人中至少有1人“支持生育二孩”的概率.
参考公式: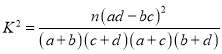 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
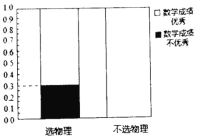
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附: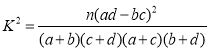
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |