题目内容

【题目】直线与圆相交于两点,当的面积达到最大时,________.

【答案】

【解析】

由圆的方程找出圆心坐标和半径,同时把直线的方程整理为一般式方程,然后利用点到直线的距离公式表示出圆心到直线的距离,即为圆中弦的弦心距,根据垂径定理得到垂足为弦的中点,由圆的半径,弦心距及弦的一半构成的直角三角形,利用勾股定理表示出弦的长度,然后利用三角形的面积公式底乘以高除,用含有的式子表示出三角形的面积,并利用基本不等式求出面积的最大值,以及面积取得最大值时的值,从而列出关于的方程,求出方程的解即可得到面积最大时的值.

解：由圆,

得到圆心坐标为 ,半径,

把直线的方程为,

整理为一般式方程得：,

.圆心到直线的距离

弦的长度,

,

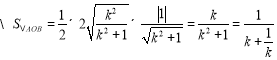又因为,

当且仅当时取等号,取得最大值,最大值为.

解得

故答案为：

练习册系列答案
相关题目

【题目】如图，四棱锥中，四边形是边长为2的菱形，

（1）证明：平面平面；

（2）当平面与平面所成锐二面角的余弦值，求直线与平面所成角正弦值.

【题目】设抛物线的焦点为，直线与抛物线交于两点.

（1）若过点，且，求的斜率；

（2）若，且的斜率为，当时，求在轴上的截距的取值范围（用表示），并证明的平分线始终与轴平行.

【题目】已知函数，

（1）若恒成立，求实数的最大值；

（2）设函数，求证：.

【题目】赵爽是我国汉代数学家、天文学家，他在注解《周髀算经》时，介绍了“勾股圆方图”，亦称“赵爽弦图”，它被2002年国际数学家大会选定为会徽.“赵爽弦图”是以弦为边长得到的正方形，该正方形由4个全等的直角三角形加上中间一个小正方形组成类比“赵爽弦图”，可类似地构造如图所示的图形它是由3个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形设DF＝2AF＝2，若在大等边三角形中随机取一点，则此点取自三个全等三角形（阴影部分）的概率是（ ）

A.B.C.D.

【题目】已知椭圆C：.

（1）求椭圆C的离心率；

（2）设分别为椭圆C的左右顶点,点P在椭圆C上,直线AP,BP分别与直线相交于点M,N.当点P运动时,以M,N为直径的圆是否经过轴上的定点？试证明你的结论.

【题目】从①前项和，②，③且，这三个条件中任选一个，补充到下面的问题中，并完成解答．

在数列中，，_______，其中．

（Ⅰ）求的通项公式；

（Ⅱ）若成等比数列，其中，且，求的最小值．

【题目】已知函数．

（1）若，证明：当时，；

（2）若在只有一个零点，求．

【题目】已知椭圆的焦点为和，过的直线交于，两点，过作与轴垂直的直线交直线于点．设，已知当时，．

（Ⅰ）求椭圆的方程；

（Ⅱ）求证：无论如何变化，直线过定点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网