题目内容
已知点P(－2,－3)和以Q为圆心的圆(x－4)2+(y－2)2=9.
(1)画出以PQ为直径,Q′为圆心的圆,再求出它的方程.
(2)作出以Q为圆心的圆和以Q′为圆心的圆的两个交点A、B.直线PA、PB是以Q为圆心的圆的切线吗?为什么?
(3)求直线AB的方程.
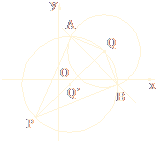
(1) x2+y2－2x+y－14=0.
(2)PA、PB是圆(x－4)2+(y－2)2=9的切线.
因为点A、B在圆x2+y2－2x+y－14=0上,且PQ是直径.
所以PA⊥AQ,PB⊥BQ.
所以PA、PB是圆(x－4)2+(y－2)2=9的切线.
(3) 直线AB的方程.6x+5y－25=0.
解析:
(1)因为P(－2,－3),Q(4,2)是以Q′为圆心的圆的直径的两个端点,所以以Q′为圆心的圆的方程是(x+2)(x－4)+(y+3)(y－2)=0,
即x2+y2－2x+y－14=0.
(2)PA、PB是圆(x－4)2+(y－2)2=9的切线.
因为点A、B在圆x2+y2－2x+y－14=0上,且PQ是直径.
所以PA⊥AQ,PB⊥BQ.
所以PA、PB是圆(x－4)2+(y－2)2=9的切线.
(3)两方程(x－4)2+(y－2)2=9、x2+y2－2x+y－14=0相减,得6x+5y－25=0.
这就是直线AB的方程.
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
相关题目