题目内容
在底面直径和高均为2R的圆锥内作一内接圆柱,当圆柱的底面半径和高分别为多少时,它的体积最大?
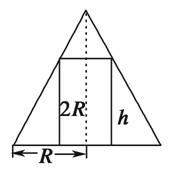
[解析] 根据题意作如图所示的截面.
设圆柱的高为h,底面半径为r(0<r<R),体积为V,
则 =
= ,
,
∴h=2(R-r),
∴V=πr2h=2πr2(R-r)=2πRr2-2πr3.
∴V′=4πRr-6πr2,由V′=0得r=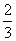 R,
R,
当r=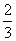 R时,圆柱的体积V取得最大值,
R时,圆柱的体积V取得最大值,
此时圆柱的高h=2(R-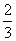 R)=
R)=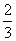 R.
R.

练习册系列答案
相关题目
题目内容
在底面直径和高均为2R的圆锥内作一内接圆柱,当圆柱的底面半径和高分别为多少时,它的体积最大?

[解析] 根据题意作如图所示的截面.
设圆柱的高为h,底面半径为r(0<r<R),体积为V,
则 =
= ,
,
∴h=2(R-r),
∴V=πr2h=2πr2(R-r)=2πRr2-2πr3.
∴V′=4πRr-6πr2,由V′=0得r=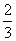 R,
R,
当r=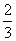 R时,圆柱的体积V取得最大值,
R时,圆柱的体积V取得最大值,
此时圆柱的高h=2(R-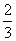 R)=
R)=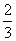 R.
R.
