题目内容
【题目】某手机生产企业为了对研发的一批最新款手机进行合理定价,将该款手机按事先拟定的价格进行试销,得到单价![]() (单位:千元)与销量
(单位:千元)与销量![]() (单位:百件)的关系如下表所示:
(单位:百件)的关系如下表所示:
单价 | 1 | 1.5 | 2 | 2.5 | 3 |
销量 | 10 | 8 | 7 | 6 |
|
已知![]() .
.
(Ⅰ)若变量![]() ,
,![]() 具有线性相关关系,求产品销量
具有线性相关关系,求产品销量![]() (百件)关于试销单价
(百件)关于试销单价![]() (千元)的线性回归方程
(千元)的线性回归方程![]() ;
;
(Ⅱ)用(Ⅰ)中所求的线性回归方程得到与![]() 对应的产品销量的估计值
对应的产品销量的估计值![]() ,当销售数据
,当销售数据![]() 对应的残差满足
对应的残差满足![]() 时,则称
时,则称![]() 为一个“好数据”,现从5个销售数据中任取3个,求其中“好数据”的个数
为一个“好数据”,现从5个销售数据中任取3个,求其中“好数据”的个数![]() 的分布列和数学期望.
的分布列和数学期望.
参考公式: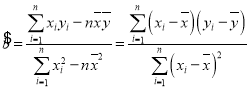 ,
,![]() .
.
【答案】(Ⅰ)![]() (Ⅱ)见解析,
(Ⅱ)见解析,![]()
【解析】
(Ⅰ)由![]() 可求出
可求出![]() ,求出
,求出![]() ,再分别计算出
,再分别计算出![]() 和
和![]() ,代入公式可求出
,代入公式可求出![]() ,由
,由![]() 求出
求出![]() ,从而得到线性回归方程;
,从而得到线性回归方程;
(Ⅱ)利用![]() 的值判断共有三个好数据,再计算对应的概率值,列出分布列,计算数学期望即可.
的值判断共有三个好数据,再计算对应的概率值,列出分布列,计算数学期望即可.
(Ⅰ)由![]() ,可得
,可得![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
代入得 ,
,
![]() ,
,
∴回归直线方程为![]() .
.
(Ⅱ)![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
共有3个“好数据”.
∴![]() ,
,
![]() ,
,![]() ,
,
∴![]() 的分布列为:
的分布列为:
| 1 | 2 | 3 |
|
|
|
|
![]() 的期望值为
的期望值为![]() .
.

【题目】2020年寒假是特殊的寒假,因为疫情全体学生只能在家进行网上在线学习,为了研究学生在网上学习的情况,某学校在网上随机抽取120名学生对线上教育进行调查,其中男生与女生的人数之比为11∶13,其中男生30人对于线上教育满意,女生中有15名表示对线上教育不满意.
(1)完成![]() 列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
列联表,并回答能否有99%的把握认为对“线上教育是否满意与性别有关”;
满意 | 不满意 | 总计 | |
男生 | |||
女生 | |||
合计 | 120 |
(2)从被调查中对线上教育满意的学生中,利用分层抽样抽取8名学生,再在8名学生中抽取3名学生,作线上学习的经验介绍,其中抽取男生的个数为![]() ,求出
,求出![]() 的分布列及期望值.
的分布列及期望值.
参考公式:附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 0.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10828 |