题目内容
【题目】设
（
，
）．
（1）若展开式中第5项与第7项的系数之比为3∶8，求k的值；
（2）设
（
），且各项系数
，
，
，…，
互不相同．现把这
个不同系数随机排成一个三角形数阵：第1列1个数，第2列2个数，…，第n列n个数．设
是第i列中的最小数，其中
，且i，．记
的概率为
．求证：
．
【答案】（1）
；（2）证明见解析.
【解析】
（1）利用题目所给展开式中第
项与第
项的系数之比列方程，解方程求得
的值.
（2）利用相互独立事件概率乘法公式，求得
的表达式，构造数列
，判断出数列
的单调性，由此证得不等式成立
（1）因为在展开式中第5项与第7项的系数之比为3∶8，即
，
所以
，即
，所以
，
解得
或．
因为
，所以．
（2）由题意，最小数在第n列的概率为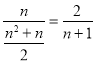
，
去掉第n列已经排好的n个数，
则余下的
个数中最小值在第
列的概率为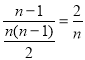
，
…………
以此类推，
余下的数中最小数在第2列的概率为
，
所以
．
由于
，所以
．
设，
所以
．
记
，所以
，
所以
是递增数列，所以
；是递增数列，所以
，
所以
，所以
，即
．
练习册系列答案
相关题目
【题目】某手机生产企业为了对研发的一批最新款手机进行合理定价，将该款手机按事先拟定的价格进行试销，得到单价
（单位：千元）与销量
（单位：百件）的关系如下表所示：
单价 | 1 | 1.5 | 2 | 2.5 | 3 |
销量 | 10 | 8 | 7 | 6 |
|
已知
.
（Ⅰ）若变量，具有线性相关关系，求产品销量（百件）关于试销单价（千元）的线性回归方程
；
（Ⅱ）用（Ⅰ）中所求的线性回归方程得到与
对应的产品销量的估计值
，当销售数据
对应的残差满足
时，则称为一个“好数据”，现从5个销售数据中任取3个，求其中“好数据”的个数
的分布列和数学期望.
参考公式：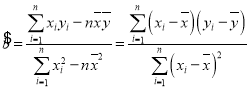
，
.
