题目内容
设集合A={x||x-a|＜1，x∈R}，B={x||x-b|＞2，x∈R}．若A⊆B，则实数a，b必满足 ．
考点：集合的包含关系判断及应用
专题：集合
分析：先通过解绝对值不等式求出集合A，B，根据A⊆B及子集的定义即可找到a，b满足的条件．
解答：
解：A={x|a-1＜x＜a+1}，B={x|x＞b+2，或x＜b-2}；
∵A⊆B；
∴b+2≤a-1，或b-2≥a+1；
∴a-b≥3，或a-b≤-3；
即|a-b|≥3．
故答案为：|a-b|≥3．
∵A⊆B；
∴b+2≤a-1，或b-2≥a+1；
∴a-b≥3，或a-b≤-3；
即|a-b|≥3．
故答案为：|a-b|≥3．
点评：考查解绝对值不等式，子集的定义，并且可借用数轴求解．
练习册系列答案
相关题目
如图，已知边长为2的等边△PCD所在的平面垂直于矩形ABCD所在的平面，BC=2命题“?x∈（0，+∞），
x3-x+1”＞0的否定是（ ）
| 1 |
| 3 |
A、?x0∉（0，+∞），
| ||
B、?x0∈（0，+∞），
| ||
C、?x0∉（0，+∞），
| ||
D、?x0∈（0，+∞），
|
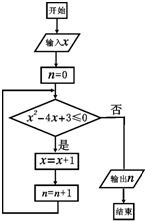在区间[-2，3]上随机选取一个数M，不变执行如图所示的程序框图，且输入x的值为1，然后输出n的值为N，则M≤N-2的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
已知（1+2i）（1-ai）=5（i为虚数单位），则实数a的值为（ ）
| A、-1 | B、1 | C、2 | D、-2 |