题目内容
5.设a、b、c∈R,且3a=4b=6c,则以下结论正确的个数为( )①若a、b、c∈R+,则3a<4b<6c
②a、b、c∈R+,则$\frac{2}{c}=\frac{1}{a}+\frac{2}{b}$
③a、b、c∈R-,则a<b<c.
| A. | 1 | B. | 2 | C. | 3 | D. | 0 |
分析 由3a=4b=6c=k>0,可得a=$\frac{lgk}{lg3}$,b=$\frac{lgk}{lg4}$,c=$\frac{lgk}{lg6}$.
①a、b、c∈R+,k>1,则lgk>0,3a=3$\frac{lgk}{lg3}$=$\frac{lgk}{lg\root{3}{3}}$,4b=4$\frac{lgk}{lg4}$=$\frac{lgk}{lg\root{4}{4}}$,6c=6$\frac{lgk}{lg6}$=$\frac{lgk}{lg\root{6}{6}}$,
通过转化为:$lg\root{3}{3}$=$lg\root{12}{{3}^{4}}$,$lg\root{4}{4}$=$lg\root{12}{{4}^{3}}$,$lg\root{6}{6}$=lg$\root{12}{{6}^{2}}$,进而得出大小关系.
②a、b、c∈R+,k>1,则$\frac{1}{a}+\frac{2}{b}$=$\frac{lg3}{lgk}$+$\frac{2lg4}{lgk}$=$\frac{lg48}{lgk}$,$\frac{2}{c}$=$\frac{2lg6}{lgk}$=$\frac{lg36}{lgk}$,即可判断出关系.
③a、b、c∈R-,则0<k<1,lgk<0,$0<\frac{1}{lg6}$<$\frac{1}{lg4}$<$\frac{1}{lg3}$.即可得出大小关系.
解答 解:由3a=4b=6c=k>0,
∴a=$\frac{lgk}{lg3}$,b=$\frac{lgk}{lg4}$,c=$\frac{lgk}{lg6}$.
①a、b、c∈R+,k>1,则lgk>0,3a=3$\frac{lgk}{lg3}$=$\frac{lgk}{lg\root{3}{3}}$,4b=4$\frac{lgk}{lg4}$=$\frac{lgk}{lg\root{4}{4}}$,6c=6$\frac{lgk}{lg6}$=$\frac{lgk}{lg\root{6}{6}}$,
∵$lg\root{3}{3}$=$lg\root{12}{{3}^{4}}$,$lg\root{4}{4}$=$lg\root{12}{{4}^{3}}$,$lg\root{6}{6}$=lg$\root{12}{{6}^{2}}$,
$\root{12}{{3}^{4}}$=$\root{12}{81}$>$\root{12}{64}$=$\root{12}{{4}^{3}}$>$\root{12}{{6}^{2}}$=$\root{6}{6}$.
∴$lg\root{3}{3}$>$lg\root{4}{4}$>$lg\root{6}{6}$>0,
∴0<$\frac{1}{lg\root{3}{3}}$<$\frac{1}{lg\root{4}{4}}$<$\frac{1}{lg\root{6}{6}}$,
∴3a<4b<6c.,因此①正确.
②a、b、c∈R+,k>1,则$\frac{1}{a}+\frac{2}{b}$=$\frac{lg3}{lgk}$+$\frac{2lg4}{lgk}$=$\frac{lg48}{lgk}$,$\frac{2}{c}$=$\frac{2lg6}{lgk}$=$\frac{lg36}{lgk}$
∴$\frac{2}{c}=\frac{1}{a}+\frac{2}{b}$不成立,因此②不正确.
③a、b、c∈R-,则0<k<1,lgk<0,$0<\frac{1}{lg6}$<$\frac{1}{lg4}$<$\frac{1}{lg3}$.
∴$\frac{lgk}{lg3}$<$\frac{lgk}{lg4}$<$\frac{lgk}{lg6}$,即a<b<c,因此③正确.
综上可得:只有①③正确.
故选:B.
点评 本题考查了对数的运算性质、对数函数的单调性、不等式的性质,考查了推理能力与计算能力,属于中档题.

| A. | (0,+∞) | B. | (0,e) | C. | [1,e) | D. | (e,+∞) |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
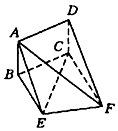 如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°.AD=$\sqrt{3}$,EF=2
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE∥CF,∠BCF=∠CEF=90°.AD=$\sqrt{3}$,EF=2