题目内容
9.有一个游戏,将标有数字1、2、3、4的四张卡片分别随机发给甲、乙、丙、丁4个人,每人一张,并请这4人在看自己的卡片之前进行预测:甲说:乙或丙拿到标有3的卡片;乙说:甲或丙拿到标有2的卡片;丙说:标有1的卡片在甲手中;丁说:甲拿到标有3的卡片.结果显示:这4人的预测都不正确,那么甲、乙、丙、丁4个人拿到的卡片上的数字依次为4、2、1、3.分析 根据预测都不正确,即可推出相对应的数字
解答 解:乙丙丁所说为假⇒甲拿4,甲乙所说为假⇒丙拿1,甲所说为假?乙拿2;
故甲、乙、丙、丁4个人拿到的卡片上的数字依次为4,2,1,3,
故答案为:4,2,1,3
点评 本题考查了合情推理的问题,关键是掌握命题的否定,属于基础题.

练习册系列答案
相关题目
20.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线被圆(x-c)2+y2=4a2截得弦长为2b(其中c为双曲线的半焦距),则该双曲线的离心率为( )
| A. | $\sqrt{6}$ | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{6}}{2}$ |
17.双曲线C的渐近线方程为y=±$\frac{{2\sqrt{3}}}{3}x$,一个焦点为F(0,-$\sqrt{7}$),点A($\sqrt{2}$,0),点P为双曲线第一象限内的点,则当P点位置变化时,△PAF周长的最小值为( )
| A. | 8 | B. | 10 | C. | $4+3\sqrt{7}$ | D. | $3+3\sqrt{17}$ |
14.执行如图所示的程序框图,则输出的s的值是( )


| A. | 7 | B. | 6 | C. | 5 | D. | 3 |
18. 某程序框图如图所示,其中$g(x)=\frac{1}{{{x^2}+x}}$,若输出的$S=\frac{2016}{2017}$,则判断框内应填入的条件为( )
某程序框图如图所示,其中$g(x)=\frac{1}{{{x^2}+x}}$,若输出的$S=\frac{2016}{2017}$,则判断框内应填入的条件为( )
 某程序框图如图所示,其中$g(x)=\frac{1}{{{x^2}+x}}$,若输出的$S=\frac{2016}{2017}$,则判断框内应填入的条件为( )
某程序框图如图所示,其中$g(x)=\frac{1}{{{x^2}+x}}$,若输出的$S=\frac{2016}{2017}$,则判断框内应填入的条件为( )| A. | n<2017 | B. | n≤2017 | C. | n>2017 | D. | n≥2017 |
19.已知实数a,b,c满足 ${(\frac{1}{3})^x}=2,{log_3}b=\frac{1}{2},{c^{-3}}=2$,则实数a,b,c的大小关系为( )
| A. | a<b<c | B. | a<c<b | C. | b<c<a | D. | b<a<c |
 工人在悬挂如图所示的一个正六边形装饰品时,需要固定六个位置上的螺丝,首先随意拧紧一个螺丝,接着拧紧距离它最远的第二个螺丝,再随意拧紧第三个螺丝,接着拧紧距离第三个螺丝最远的第四个螺丝,第五个和第六个以此类推,则不同的固定方式有48种.
工人在悬挂如图所示的一个正六边形装饰品时,需要固定六个位置上的螺丝,首先随意拧紧一个螺丝,接着拧紧距离它最远的第二个螺丝,再随意拧紧第三个螺丝,接着拧紧距离第三个螺丝最远的第四个螺丝,第五个和第六个以此类推,则不同的固定方式有48种.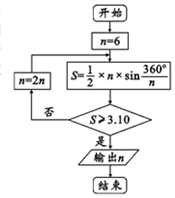 公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( )
公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( )