题目内容
平面直角坐标系中有两个动点A、B,他们的起始坐标分别是(0,0),(2,2),动点A,B从同一时刻开始每隔1秒钟向上、下、左、右四个方向中的一个方向移动一个单位.已知动点A向左、右移动1个单位的概率都是 ,向上移动一个单位的概率是
,向上移动一个单位的概率是 ,向下移动一个单位的概率是p; 动点B向上、下、左、右移动一个单位的概率都是q.
,向下移动一个单位的概率是p; 动点B向上、下、左、右移动一个单位的概率都是q.(1)求p和q的值.
(2)试判断最少需要几秒钟,动点A、B能同时到达点D(1,2),并求在最短时间内它们同时到达点D的概率.
【答案】分析:(1)由于质点向四个方向移动的概率之和为1,故可得结论;
(2)质点A至少需要经过3秒才能到达D点,质点B至少需要1秒才能到达D点,所以至少需要3秒,A,B才能同时到达点D(1,2),质点A经过3秒到达D点有三条路径,但均为向上移动两步,向右移动一步;质点B经过3秒到达D点有9条路径,由于A,B相互独立,所以分别计算概率再相乘即可.
解答:解:(1)由已知得: +
+ +
+ +p=1,∴p=
+p=1,∴p= ,
,
又由 4q=1得,q= ;
;
(2)质点A至少需要经过3秒才能到达D点,质点B至少需要1秒才能到达D点,所以至少需要3秒,A,B才能同时到达点D(1,2)
质点A经过3秒到达D点的概率为 =
=
质点B经过3秒到达D点的概率为9( )3=
)3=
因为A,B相互独立,所以它们同时到达C点的概率为 =
= .
.
点评:本题考查概率的应用问题,考查学生分析解决问题的能力,属于中档题.
(2)质点A至少需要经过3秒才能到达D点,质点B至少需要1秒才能到达D点,所以至少需要3秒,A,B才能同时到达点D(1,2),质点A经过3秒到达D点有三条路径,但均为向上移动两步,向右移动一步;质点B经过3秒到达D点有9条路径,由于A,B相互独立,所以分别计算概率再相乘即可.
解答:解:(1)由已知得:
 +
+ +
+ +p=1,∴p=
+p=1,∴p= ,
,又由 4q=1得,q=
 ;
;(2)质点A至少需要经过3秒才能到达D点,质点B至少需要1秒才能到达D点,所以至少需要3秒,A,B才能同时到达点D(1,2)
质点A经过3秒到达D点的概率为
 =
=
质点B经过3秒到达D点的概率为9(
 )3=
)3=
因为A,B相互独立,所以它们同时到达C点的概率为
 =
= .
.点评:本题考查概率的应用问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 中有两定点
中有两定点 ,
, ,若动点M满足
,若动点M满足 ,设动点M的轨迹为C。
,设动点M的轨迹为C。 交曲线C于A、B两点,交直线
交曲线C于A、B两点,交直线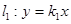 于点D,若
于点D,若 ,证明:D为AB的中点。
,证明:D为AB的中点。 中有两定点
中有两定点 ,
, ,若动点M满足
,若动点M满足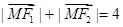 ,设动点M的轨迹为C。
,设动点M的轨迹为C。 交曲线C于A、B两点,交直线
交曲线C于A、B两点,交直线 于点D,若
于点D,若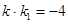 ,证明:D为AB的中点。
,证明:D为AB的中点。