题目内容
(本小题满分12分)
在平面直角坐标系 中有两定点
中有两定点 ,
, ,若动点M满足
,若动点M满足 ,设动点M的轨迹为C。
,设动点M的轨迹为C。
(1)求曲线C的方程;
(2)设直线 交曲线C于A、B两点,交直线
交曲线C于A、B两点,交直线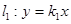 于点D,若
于点D,若 ,证明:D为AB的中点。
,证明:D为AB的中点。
【答案】
(1)曲线C的方程为
(2)略
【解析】解:(1)设动点M的坐标为

由椭圆定义可知,点M的轨迹C是以 )为焦点,
)为焦点,
长半轴长为2的椭圆,它的短半轴长 …………4分
…………4分
故 曲线C的方程为 …………5分
…………5分
(Ⅱ)依题意,联立方程组
消去 得:
得: …………7分
…………7分

即AB的中点坐标为 …………9分
…………9分
解方程组
得直线 与
与 的交点D的坐标为
的交点D的坐标为 …………10分
…………10分
由 得
得 ,代入D点坐标即为
,代入D点坐标即为
综上可知,D为AB的中点…………12分

练习册系列答案
相关题目