题目内容

已知 $数学公式$ ．
（Ⅰ）求f（x）的最小正周期；
（Ⅱ）求f（x）在区间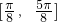 $数学公式$ 上的最大值，并求出f（x）取最大值时x的值．

解：（Ⅰ） $\text{[math]}$
= $\text{[math]}$ = $\text{[math]}$
故f（x）的周期是π．
（Ⅱ）∵ $\text{[math]}$ ， $\text{[math]}$
∴ $\text{[math]}$ 上是减函数，
∴ $\text{[math]}$ 上是增函数
∴ $\text{[math]}$
故当 $\text{[math]}$ 时，f（x）的最大值是 $\text{[math]}$
分析：（Ⅰ）利用诱导公式和和差化积公式对函数解析式进行化简为f（x）= $\text{[math]}$ ，即可求得f（x）的最小正周期；
（Ⅱ）根据 $\text{[math]}$ ，求出 $\text{[math]}$ ，利用余弦函数的单调性即可求得结果．
点评：本题考查三角恒等变换和三角函数的周期性以及最值问题，利用公式对三角函数解析式化简是解题的关键，考查运算能力，属中档题．

练习册系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

53English系列答案

考纲强化阅读系列答案

相关题目

．
（Ⅰ）求f（x）的最小正周期，并求其单调递增区间；
（Ⅱ）当

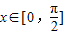时，求f（x）的值域．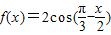

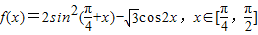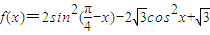
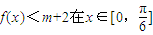（1）求f（x）的单调递增区间；
（2）若x∈[-π，π]求f（x）的最大值和最小值．

．
（Ⅰ）求f（x）的最大值和最小值；
（Ⅱ）若不等式|f（x）-m|＜2在定义域上恒成立，求实数m的取值范围．

（I）求f（x）最小正周期和单调递减区间；
（II）若

上恒成立，求实数m的取值范围．

．
（Ⅰ）求f（x）的最大值和最小值；
（Ⅱ）若不等式|f（x）-m|＜2在定义域上恒成立，求实数m的取值范围．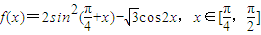