Question

已知函数．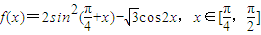
（Ⅰ）求f（x）的最大值和最小值；
（Ⅱ）若不等式|f（x）-m|＜2在定义域上恒成立，求实数m的取值范围．

Answer 1

【答案】分析：（Ⅰ）利用二倍角公式和两角和公式对函数的解析式进行化简整理，进而根据x的范围和正弦函数的单调性求得函数的最大和最小值．
（Ⅱ）问题转化为f（x）-2＜m＜f（x）+2恒成立，进而利用（1）中函数的最大值和最小值，推断出m＞f（x）_max-2且m＜f（x）_min+2，求得m的范围．
解答：解：（Ⅰ）∵=．
又∵，
∴，
即，
∴f（x）_max=3，f（x）_min=2．

（Ⅱ）∵|f（x）-m|＜2?f（x）-2＜m＜f（x）+2，，
∴m＞f（x）_max-2且m＜f（x）_min+2，
∴1＜m＜4，即m的取值范围是（1，4）．
点评：本小题主要考查三角函数和不等式的基本知识，以及运用三角公式、三角函数的图象和性质解题的能力．