题目内容
8.设p:|4x-3|≤1;q:x2-(2a+1)x+a2+a≤0,若p是q的充分不必要条件,求a的取值范围.分析 根据一元二次不等式的解法分别求出命题p和q,由p是q的充分不必要条件,可知p⇒q,从而求出a的范围:
解答 解:因为|4x-3|≤1,所以$\frac{1}{2}$≤x≤1,即p:$\frac{1}{2}$≤x≤1.
由x2-(2a+1)x+a2+a≤0,
得(x-a)[(x-(a+1)]≤0,
所以a≤x≤a+1,因为p是q的充分不必要条件,
所以p⇒q,q推不出p.
所以$\left\{\begin{array}{l}{a+1>1}\\{a≤\frac{1}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{a+1≥1}\\{a<\frac{1}{2}}\end{array}\right.$
解得0≤a≤$\frac{1}{2}$.
所以a的取值范围是[0,$\frac{1}{2}$].
点评 本题考查充分条件、必要条件和充要条件,解题时要认真审题,仔细解答,注意不等式组的解法,此题是一道基础题;

练习册系列答案
相关题目
18.对于常数k定义fk(x)=$\left\{\begin{array}{l}f(x),f(x)≥k\\ k,f(x)<k\end{array}$,若f(x)=x-lnx,则f3(f2(e))=( )
| A. | 3 | B. | e+1 | C. | e | D. | e-1 |
16.已知点P为不等式组$\left\{\begin{array}{l}x-2y+1≥0\\ x≤2\\ x+y-1≥0\end{array}\right.$所表示的平面区域内的一点,点Q是圆M:(x+1)2+y2=1上的一个动点,则|PQ|的最大值是( )
| A. | $\frac{{3\sqrt{5}+2}}{2}$ | B. | $\frac{{2\sqrt{5}+3}}{3}$ | C. | $\frac{{2\sqrt{5}}}{3}$ | D. | $\sqrt{10}$ |
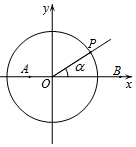 如图,在平面直角坐标系中,点$A(-\frac{1}{2},0)$,$B(\frac{3}{2},0)$,锐角α的终边与单位圆O交于点P.
如图,在平面直角坐标系中,点$A(-\frac{1}{2},0)$,$B(\frac{3}{2},0)$,锐角α的终边与单位圆O交于点P.