题目内容
18.对于常数k定义fk(x)=$\left\{\begin{array}{l}f(x),f(x)≥k\\ k,f(x)<k\end{array}$,若f(x)=x-lnx,则f3(f2(e))=( )| A. | 3 | B. | e+1 | C. | e | D. | e-1 |
分析 利用分段函数的解析式,对所求的表达式由里及外逐步求解即可.
解答 解:f(x)=x-lnx,f(e)=e-lne=e-1<k=2,
∴f2(e)=2,
又∵f(2)=2-ln2<k=3,
∴f3(f2(e))=f3(2)=3.
故选:A.
点评 本题考查分段函数的应用,函数的值的求法,考查计算能力.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14.如图所示的程序框图中,如输入m=4,t=3,则输出y=( )
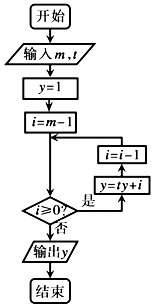

| A. | 61 | B. | 62 | C. | 183 | D. | 184 |
7.将函数y=cos(2x+$\frac{π}{3}$)的图象向左平移$\frac{π}{6}$个单位后,得到f(x)的图象,则( )
| A. | f(x)=-sin 2x | B. | f(x)的图象关于x=-$\frac{π}{3}$对称 | ||
| C. | f($\frac{7π}{3}$)=$\frac{1}{2}$ | D. | f(x)的图象关于(1,0)对称 |
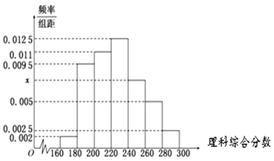 某重点中学100位学生在市统考中的理科综合分数,以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.
某重点中学100位学生在市统考中的理科综合分数,以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300]分组的频率分布直方图如图.