题目内容
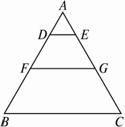
如图1-3-4，已知△ABC中，AB =AC，AD是BC边上的中线，CF∥BA，BF交AD于P点，交AC于E点.求证:BP2=PE·PF.
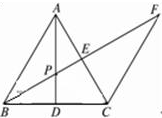
图1-3-4
思路解析:因为BP、PE、PF三条线段共线，找不到两个三角形，所以必须考虑等线段代换等其他方法，因为AB =AC，D是BC中点，由等腰三角形的性质知AD是BC的垂直平分线，如果我们连结PC，由线段垂直平分线的性质知PB =PC，只需证明△PEC∽△PCF，问题就能解决了.
图1-3-5
证明:连结PC，在△ABC中，?
∵AB =AC，D为BC中点，?
∴AD垂直平分BC.?
∴PB =PC.?
∴∠1=∠2.?
∵AB =AC，?
∴∠ABC =∠ACB.?
∴∠ABC-∠1=∠ACB-∠2.?
∴∠3=∠4.?
∵CF∥AB，?
∴∠3=∠F.?
∴∠4=∠F.?
又∵∠EPC=∠CPF，?
∴△PCE∽△PFC.?
∴
=
.?
∴PC2 =PE·PF.?
∵PC =PB，?
∴PB2 =PE·PF.
练习册系列答案
阅读快车系列答案
相关题目
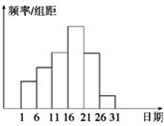在学校开展的综合实践活动中，某班进行了小制作评比，作品上交时间为5月1日至30日，评委会把同学们上交作品的件数按5天一组分组统计，绘制了频率分布直方图（如图所示），已知从左到右各长方形高的比为2：3：4：6：4：1，第三组的频数为12，则本次活动参加评比作品总数、上交的作品数量最多的组的作品件数依次为（ ）
