题目内容
16.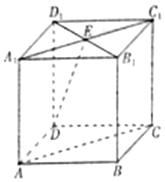 如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=$\frac{\sqrt{6}}{6}$.
如图所示,在正方体AC1中,AB=2,A1C1∩B1D1=E,直线AC与直线DE所成的角为α,直线DE与平面BCC1B1所成的角为β,则cos(α-β)=$\frac{\sqrt{6}}{6}$.
分析 由AC∥A1E,知α=∠A1ED,过E作EF⊥平面ADD1A1,交A1D1于F,则β=∠EDF,由此能求出cos(α-β)的值.
解答 解:∵在正方体AC1中,AB=2,A1C1∩B1D1=E,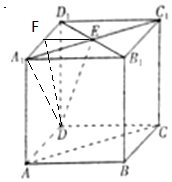
AC∥A1E,直线AC与直线DE所成的角为α,
∴α=∠A1ED,且A1E=$\frac{1}{2}\sqrt{4+4}$=$\sqrt{2}$,DE=$\sqrt{4+2}=\sqrt{6}$,A1D=$\sqrt{4+4}=2\sqrt{2}$,
∴cosα=$\frac{{A}_{1}{E}^{2}+D{E}^{2}-{A}_{1}{D}^{2}}{2×{A}_{1}E×DE}$=$\frac{2+6-8}{2×\sqrt{2}×\sqrt{6}}$=0,sinα=1,
过E作EF⊥平面ADD1A1,交A1D1于F,则F是A1D1的中点,
∵平面ADD1A1∥平面BCC1B1,直线DE与平面BCC1B1所成的角为β,
∴β=∠EDF,且EF=1,DF=$\sqrt{4+1}=\sqrt{5}$,
sinβ=$\frac{EF}{DE}$=$\frac{\sqrt{6}}{6}$,cosβ=$\frac{DF}{DE}$=$\frac{\sqrt{5}}{\sqrt{6}}$,
∴cos(α-β)=cosαcosβ+sinαsinβ=0×$\frac{\sqrt{5}}{\sqrt{6}}$+1×$\frac{\sqrt{6}}{6}$=$\frac{\sqrt{6}}{6}$.
故答案为:$\frac{{\sqrt{6}}}{6}$.
点评 本题考查两角差的余弦值的求法,考查余弦定理、勾股定理的应用,考查推理论证能力、运算求解能力、空间思维能力,考查函数与方程思想、化归转化思想、数形结合思想,是中档题.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
| A. | ∅ | B. | {x|1<x≤3} | C. | {x|1<x<3} | D. | {x|1≤x<3} |
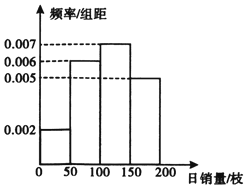 某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.
某鲜花店根据以往某品种鲜花的销售记录,绘制出日销售量的频率分布直方图,如图所示.将日销售量落入各组区间的频率视为概率,且假设每天的销售量相互独立.