题目内容
15．等差数列{an}前n项和为Sn，S7+S5=10，a3=5，则S7=（ ）| A． | 25 | B． | 49 | C． | -15 | D． | 40 |
分析 利用等差数列的通项公式和前n项和公式列出方程组，求出首项和公差，由此能求出S7．
解答 解：∵等差数列{an}前n项和为Sn，S7+S5=10，a3=5，
∴$\left\{\begin{array}{l}{7{a}_{1}+\frac{7×6}{2}d+5{a}_{1}+\frac{5×4}{2}d=10}\\{{a}_{1}+2d=5}\end{array}\right.$，
解得${a}_{1}=\frac{135}{7}$，d=-$\frac{50}{7}$，
∴S7=$7{a}_{1}+\frac{7×6}{2}d$=$7×\frac{135}{7}+\frac{7×6}{2}×（-\frac{50}{7}）$=-15．
故选：C．
点评 本题考查等差数列的性质，考查推理论证能力、运算求解能力，考查函数与方程思想、化归转化思想，是基础题．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
如图所示：湖面上甲、乙、丙三艘船沿着同一条直线航行，某一时刻，甲船在最前面的A点处，乙船在中间B点处，丙船在最后面的C点处，且BC：AB=3：1．一架无人机在空中的P点处对它们进行数据测量，在同一时刻测得∠APB=30°，∠BPC=90°．（船只与无人机的大小及其它因素忽略不计）
20．已知长方体ABCD-A1B1C1D1中，$A{A_1}=AB=\sqrt{3}$，AD=1，则异面直线B1C和C1D所成角的余弦值为（ ）
| A． | $\frac{{\sqrt{6}}}{4}$ | B． | $\frac{{\sqrt{6}}}{3}$ | C． | $\frac{{\sqrt{2}}}{6}$ | D． | $\frac{{\sqrt{3}}}{6}$ |
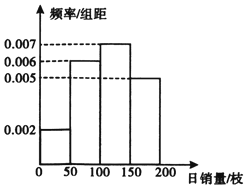某鲜花店根据以往某品种鲜花的销售记录，绘制出日销售量的频率分布直方图，如图所示．将日销售量落入各组区间的频率视为概率，且假设每天的销售量相互独立．