题目内容
（1）用综合法证明：
(
)
（2）用反证法证明：若
均为实数，且
，
，
求证：中至少有一个大于0
（1）详见解析，（2）详见解析.
解析试题分析：（1）综合法证明，实质先按分析法分析，再按综合法的写法. 
（2）反证法证明,关键在于正确假设:假设都不大于0，则
，又
,两者矛盾，故假设错误。从而中至少有一个大于0.
解：(1)
------1分
------3分
即
------5分
当且仅当
时取等号------7分
(2)证明：假设都不大于0------8分
即
，
，
同时成立
则
11分
矛盾 14分
假设不成立原命题成立。 15分
考点：综合法，反证法
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
＋
＋
＋…＋
的值．
都是正实数，且
.求证：
与
中至少有一个成立.
，
是函数
的两个零点，其中常数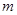
，
，设
．
表示
，
；
；
．
，
，
不能为同一等差数列中的三项．
满足
，
．
、
、
；
的表达式；
，求
．
，根据这些结果，猜想出的一般结论是 ．