题目内容
19.已知函数f(x)=$\left\{\begin{array}{l}{x+\frac{1}{x},x>0}\\{{log}_{\frac{1}{2}}|x|,x<0}\end{array}\right.$,若方程f(x2-x)=a有六个根,则实数a的取值范围是( )| A. | (1,2) | B. | (-1,2) | C. | (1,+∞) | D. | (2,+∞) |
分析 令x2-x=t,得出关于x的方程x2-x=t的解得分布情况,作出f(t)的函数图象,讨论关于t的方程f(t)=a的解得情况,从而得出方程f(x2-x)=a的解的个数.
解答 解:f(x)的定义域为{x|x≠0},
令x2-x=t(x≠0),则t≥-$\frac{1}{4}$,
且t=-$\frac{1}{4}$或t=0时,方程x2-x=t只有一解,
当-$\frac{1}{4}$<t<0或t>0时,方程x2-x=t有两解,
∴f(t)=$\left\{\begin{array}{l}{t+\frac{1}{t},t>0}\\{lo{g}_{\frac{1}{2}}(-t),-\frac{1}{4}≤t<0}\end{array}\right.$,
∴f(t)在[-$\frac{1}{4}$,0)上单调递增,在(0,1)上单调递减,在(1,+∞)上单调递增,
作出y=f(t)的函数图象如图所示:
由图象可知,当a<2时,关于t的方程f(t)=a无解,
∴方程f(x2-x)=a无解,不符合题意;
当a=2时,关于t的方程f(t)=a有两解t1=-$\frac{1}{4}$,t2=1,
∵x2-x=-$\frac{1}{4}$只有一解,x2-x=1有两解,
∴方程f(x2-x)=a有三解,不符合题意;
当a>2时,关于t的方程f(t)=a有三解,不妨从t1<t2<t3,
显然-$\frac{1}{4}$<t1<0,0<t2<1,t3>1,
又关于x的方程x2-x=ti(i=1,2,3)都有两解,
∴方程f(x2-x)=a有六解,符合题意.
故选D.
点评 本题考查了方程的根与函数图象的关系,属于中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
9.在测试中,客观题难度的计算公式为Pi=$\frac{{R}_{i}}{N}$,其中Pi为第i题的难度,Ri为答对该题的人数,N为参加测试的总人数.
现对某校髙三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如表所示:
测试后,从中随机抽取了10名学生,将他们编号后统计各题的作答情况,如表所示(“√”表示答对,“×”表示答错):
(I)根据题中数据,将抽样的10名学生每道题实测的答对人数及相应的实测难度填入表,并估计这120名学生中第5题的实测答对人数;
(Ⅱ)从编号为1到5的5人中随机抽取2人,求恰好有1人答对第5题的概率;
(Ⅲ)定义统计量S=$\frac{1}{n}$[(P′1-P1)2+(P′2-P2)2+…+(P′n-Pn)2],其中P′i为第i题的实测难度,Pi为第i题的预估难度(i=l,2,…,n),规定:若S<0.05,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
现对某校髙三年级120名学生进行一次测试,共5道客观题.测试前根据对学生的了解,预估了每道题的难度,如表所示:
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 考前预估难度Pi | 0.9 | 0.8 | 0.7 | 0.6 | 0.4 |
| 题号 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | × | √ | √ | √ | √ |
| 2 | √ | √ | √ | √ | × |
| 3 | √ | √ | √ | √ | × |
| 4 | √ | √ | √ | × | × |
| 5 | √ | √ | √ | √ | √ |
| 6 | √ | × | × | √ | × |
| 7 | × | √ | √ | √ | × |
| 8 | √ | × | × | × | × |
| 9 | √ | √ | √ | × | × |
| 10 | √ | √ | √ | √ | × |
| 题号 | 1 | 2 | 3 | 4 | 5 |
| 实测答对人数 | |||||
| 实测难度 |
(Ⅲ)定义统计量S=$\frac{1}{n}$[(P′1-P1)2+(P′2-P2)2+…+(P′n-Pn)2],其中P′i为第i题的实测难度,Pi为第i题的预估难度(i=l,2,…,n),规定:若S<0.05,则称该次测试的难度预估合理,否则为不合理.判断本次测试的难度预估是否合理.
10.函数f(x)=lnx与函数g(x)=ax2-a的图象在点(1,0)的切线相同,则实数a的值为( )
| A. | 1 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{2}$或-$\frac{1}{2}$ |
14.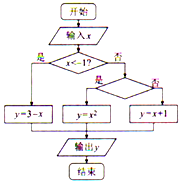 已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )
已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )
 已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )
已知分段函数y=$\left\{\begin{array}{l}{3-x,x<-1}\\{{x}^{2},-1≤x≤1}\\{x+1,x>1}\end{array}\right.$,若执行如图所示的程序框图,则框图中的条件应该填写( )| A. | x≥1? | B. | x≥-1? | C. | -1≤x≤2? | D. | x≤1? |
11.数列{an}满足a1=2,an+1=$\frac{1}{{1-{a_n}}}(n∈{N^+})$,则a2017=( )
| A. | -2 | B. | -1 | C. | 2 | D. | $\frac{1}{2}$ |
8.己知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{3}$=1(a>0)的一个焦点与抛物线y2=8x的焦点重合,则a=( )
| A. | $\sqrt{19}$ | B. | $\sqrt{13}$ | C. | 2 | D. | 1 |