题目内容
11．若f（x）=ex+sinx-cosx的导数为f'（x），则f'（0）等于（ ）| A． | 2 | B． | ln2+1 | C． | ln2-1 | D． | ln2+2 |
分析 根据题意，由f（x）的解析式计算可得f′（x）=ex+cosx+sinx，将x=0代入计算可得f'（0），即可得答案．
解答 解：根据题意，f（x）=ex+sinx-cosx，则f′（x）=ex+cosx+sinx，
则f'（0）=e0+cos0+sin0=2；
故选：A．
点评 本题考查导数的计算，关键是正确计算函数f（x）的导数．
练习册系列答案
相关题目
1．椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$，F1，F2为椭圆的左、右焦点，O为坐标原点，点P为椭圆上一点，$|OP|=\frac{{\sqrt{2}}}{4}a$，且|PF1|，|F1F2|，|PF2|成等比数列，则椭圆的离心率为（ ）
| A． | $\frac{{\sqrt{2}}}{4}$ | B． | $\frac{{\sqrt{2}}}{3}$ | C． | $\frac{{\sqrt{6}}}{3}$ | D． | $\frac{{\sqrt{6}}}{4}$ |
2．如图画的某几何体的三视图，网格纸上小正方形的边长为1，则该几何体的表面积为（ ）
| A． | $144+2\sqrt{10}π$ | B． | $144+（{2\sqrt{10}-2}）π$ | C． | $128+2\sqrt{10}π$ | D． | $128+（{2\sqrt{10}-2}）π$ |
19．已知某几何体的三视图如图所示，则该几何体的体积为（ ）
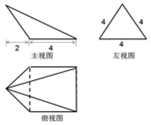
| A． | $\frac{32}{3}$ | B． | $\frac{{16\sqrt{3}}}{3}$ | C． | $\frac{{32\sqrt{3}}}{3}$ | D． | $\frac{{64\sqrt{3}}}{3}$ |
6．某校为了解学生对正在进行的一项教学改革的态度，从500名高一学生和400名高二学生中按分层抽样的方式抽取了45名学生进行问卷调查，结果可以分成以下三类：支持、反对、无所谓，调查结果统计如下：
（1）（i）求出表中的x，y的值；
（ii）从反对的同学中随机选取2人进一步了解情况，求恰好高一、高二各1人的概率；
（2）根据表格统计的数据，完成下面的2×2的列联表，并判断是否有90%的把握认为持支持与就读年级有关．（不支持包括无所谓和反对）
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
| 支持 | 无所谓 | 反对 | |
| 高一年级 | 18 | x | 2 |
| 高二年级 | 10 | 6 | y |
（ii）从反对的同学中随机选取2人进一步了解情况，求恰好高一、高二各1人的概率；
（2）根据表格统计的数据，完成下面的2×2的列联表，并判断是否有90%的把握认为持支持与就读年级有关．（不支持包括无所谓和反对）
| 高一年级 | 高二年级 | 总计 | |
| 支持 | |||
| 不支持 | |||
| 总计 |
| P（K2≥k0） | 0.10 | 0.05 | 0.01 |
| k0 | 2.706 | 3.841 | 6.635 |
16．若tanα=$\frac{1}{3}$，则sin4α-cos4α+6sin$\frac{α}{2}$cos$\frac{α}{2}$cosα=（ ）
| A． | 1 | B． | $\frac{1}{3}$ | C． | $\frac{1}{9}$ | D． | $\frac{1}{10}$ |